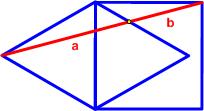
 This turned out to be a challenging geometric problem from Poo-Sung Park posted at the Twitter site #GeometryProblem
This turned out to be a challenging geometric problem from Poo-Sung Park posted at the Twitter site #GeometryProblem
“Geometry Problem 92: What is the ratio of a:b?”
See the Envelope Puzzle for solutions.

 This turned out to be a challenging geometric problem from Poo-Sung Park posted at the Twitter site #GeometryProblem
This turned out to be a challenging geometric problem from Poo-Sung Park posted at the Twitter site #GeometryProblem
“Geometry Problem 92: What is the ratio of a:b?”
See the Envelope Puzzle for solutions.
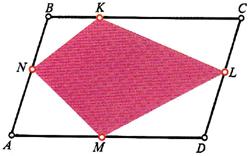 Here is another problem from the Quantum magazine, only this time from the “Challenges” section (these are expected to be a bit more difficult than the Brainteasers).
Here is another problem from the Quantum magazine, only this time from the “Challenges” section (these are expected to be a bit more difficult than the Brainteasers).
“A quadrangle is inscribed in a parallelogram whose area is twice that of the quadrangle. Prove that at least one of the quadrangle’s diagonals is parallel to one of the parallelogram’s sides. (E. Sallinen)”
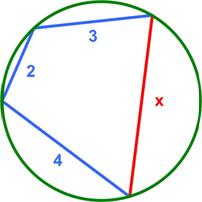
Here is another Brain Bogglers problem from 1987 by Michael Stueben.
“A quadrilateral with sides three, two, and four units in length is inscribed in a circle of diameter five. What’s the length of the fourth side of the quadrilateral?”
Like a number of other Brain Bogglers this problem also uses an insight that makes the solution easy.
See the Quad in Circle Problem for a solution.
 Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine.
“Prove that the area of the red portion of the star is exactly half the area of the whole star. (N. Avilov)”
This is a relatively simple problem, but I wanted to include it because of its cartoon. Its implied gentle post-Soviet humor reminded me of that strange decade in US-Russian affairs between the end of the Cold War and the rise of Putin in the 21st century. The strangeness was brought home when we had our annual security checks of our classified document storage. Being mostly anti-submarine warfare (ASW) material the main concern was that it would not fall into the hands of the Soviets. But with the “demise” of the Soviet Union in 1989 no one cared any more about the classification. After decades of painfully securing these documents we could not suddenly turn them loose and throw them into the public trash. So we kept them secure anyway. You can imagine how we old cold-warriors feel about the current regime.
That is not to say that I didn’t welcome the thaw. Russian literature, both classical and even “Soviet realism”, as well as Russian cinema, is some of the world’s best. And Russian mathematicians have always been superior, and especially adept at communicating with novices. The collaboration of the American mathematicians and Kvant contributors in Quantum produced excellent results during the thaw. It is unfortunate that it could not survive the rise of Putin and his oligarchs.
See the Red Star
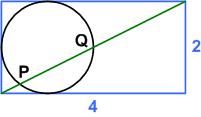 Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution:
Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution:
“The diagram shows a circle of radius 1 touching three sides of a 2 x 4 rectangle. A diagonal of the rectangle intersects the circle at P and Q, as shown.
What is the length of the chord PQ?
__A_√5____B_4/√5____C_√5 – 2/√5____D_5√5/6____E_2”
See the Circle in Slot Problem for a solution.
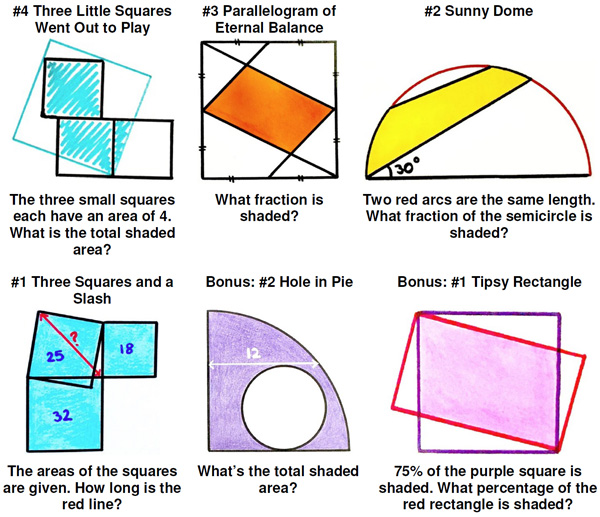
Having fallen under the spell of Catriona Shearer’s geometric puzzles again, I thought I would present the latest group assembled by Ben Orlin, which he dubs “Felt Tip Geometry”, along with a bonus of two more recent ones that caught my fancy as being fine examples of Shearer’s laconic style. Orlin added his own names to the four he assembled and I added names to my two, again ordered from easier to harder.
See Geometric Puzzle Munificence.
(Update 4/16/2020) Ben Orlin has another set of Catriona Shearer puzzles 11 Geometry Puzzles That Drive Mathematicians to Madness which I will leave you to see and enjoy. But I wanted to emphasize some observations he included that I think are spot on. Continue reading
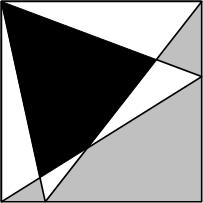 This is a problem from a while back (2015) at Futility Closet.
This is a problem from a while back (2015) at Futility Closet.
“Which part of this square has the greater area, the black part or the gray part?”
See Modern Art. for solutions.
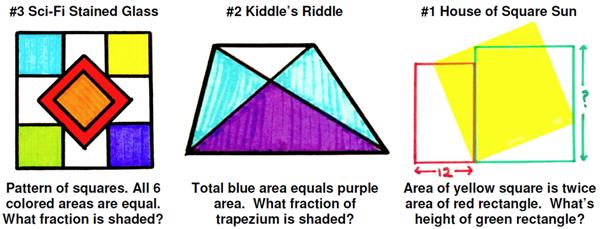 I have been subverted again by a recent post by Ben Orlin, “Geometry Puzzles for a Winter’s Day,” which is another collection of Catriona Shearer’s geometric puzzles, this time her favorites for the month of November 2019 (which Orlin seems to have named himself). I often visit Orlin’s blog, “Math with Bad Drawings”, so it is hard to kick my addiction to Shearer’s puzzles if he keeps presenting collections. Her production volume is amazing, especially as she is able to maintain the quality that makes her problems so special.
I have been subverted again by a recent post by Ben Orlin, “Geometry Puzzles for a Winter’s Day,” which is another collection of Catriona Shearer’s geometric puzzles, this time her favorites for the month of November 2019 (which Orlin seems to have named himself). I often visit Orlin’s blog, “Math with Bad Drawings”, so it is hard to kick my addiction to Shearer’s puzzles if he keeps presenting collections. Her production volume is amazing, especially as she is able to maintain the quality that makes her problems so special.
The Stained Glass puzzle generated some discussion about needed constraints to ensure a solution. Essentially, it was agreed to make explicit that the drawing had vertical and horizontal symmetry in the shapes, that is, flipping it horizontally or vertically kept the same shapes, though some of the colors might be swapped.
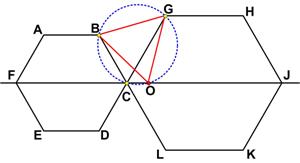 This is truly an amazing result from Five Hundred Mathematical Challenges.
This is truly an amazing result from Five Hundred Mathematical Challenges.
“Problem 119. Two unequal regular hexagons ABCDEF and CGHJKL touch each other at C and are so situated that F, C, and J are collinear.
Show that
(i) the circumcircle of BCG bisects FJ (at O say);
(ii) ΔBOG is equilateral.”
I wonder how anyone ever discovered this.
See the Magic Hexagons
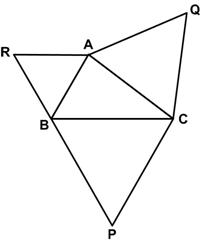 Here is another simple problem from Futility Closet.
Here is another simple problem from Futility Closet.
“Draw an arbitrary triangle [ABC] and build an equilateral triangle on each of its sides, as shown. Now show that [straight lines] AP = BQ = CR.”