 This is a nifty problem from Presh Talwakar.
This is a nifty problem from Presh Talwakar.
“This is adapted from the 1994 Putnam, A2. Thanks to Nirman for the suggestion!
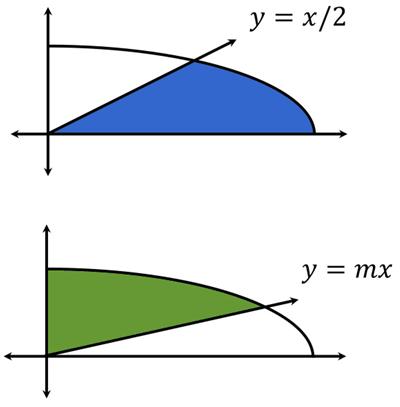
Let R be the region in the first quadrant bounded by the x-axis, the line y = x/2, and the ellipse x2/9 + y2 = 1. Let R‘ be the region in the first quadrant bounded by the y-axis, the line y = mx and the ellipse. Find the value of m such that R and R‘ have the same area.”
See the Putnam Ellipse Areas Problem for solution.

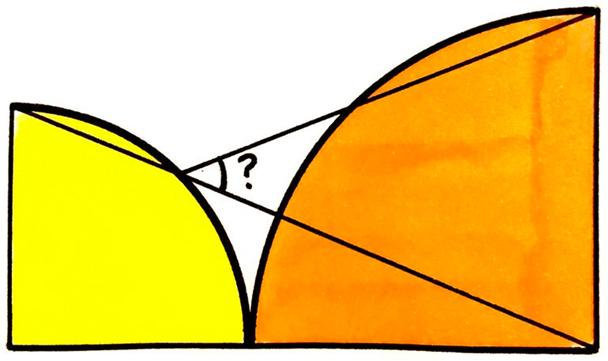 This is a Catriona Agg problem presented by itself, since it turned out to be the most challenging one I ever tried. Usually I can solve her problems in a few minutes or maybe hours, or sometimes days if they are especially challenging. But this problem has taken me weeks and I had to rely on a non-geometric argument. The problem is full of fascinating and unexpected relationships, but I couldn’t find a way to use them to prove the answer.
This is a Catriona Agg problem presented by itself, since it turned out to be the most challenging one I ever tried. Usually I can solve her problems in a few minutes or maybe hours, or sometimes days if they are especially challenging. But this problem has taken me weeks and I had to rely on a non-geometric argument. The problem is full of fascinating and unexpected relationships, but I couldn’t find a way to use them to prove the answer.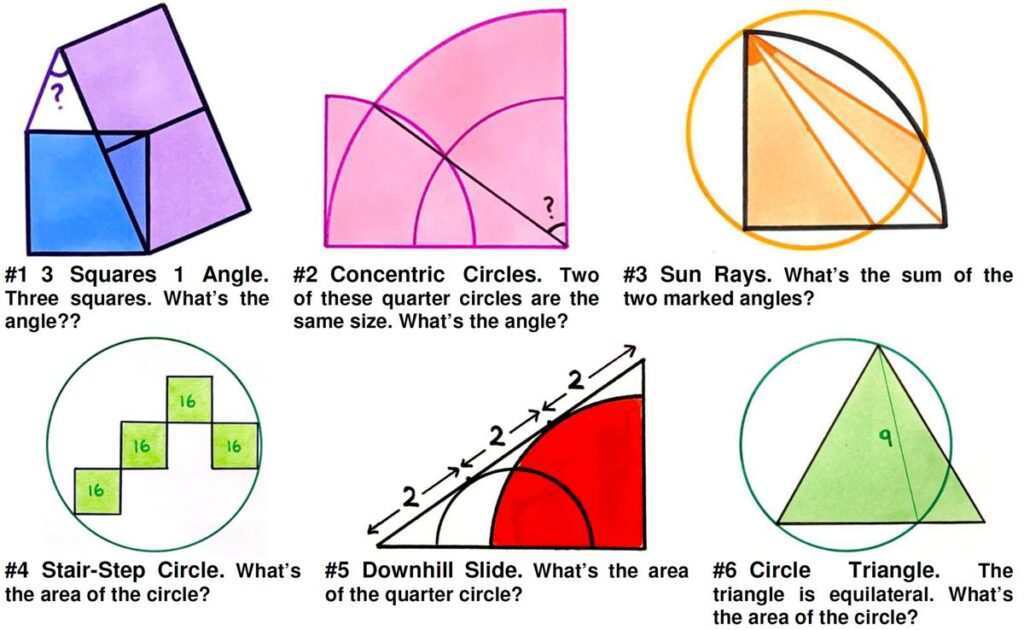 Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer).
Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer).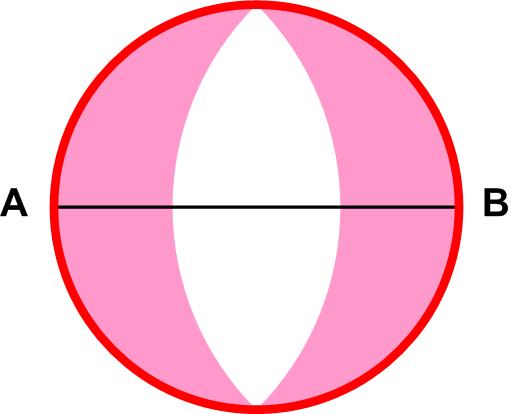 This is a straight-forward problem from the Scottish Mathematical Council (SMC) Senior Mathematics Challenge.
This is a straight-forward problem from the Scottish Mathematical Council (SMC) Senior Mathematics Challenge.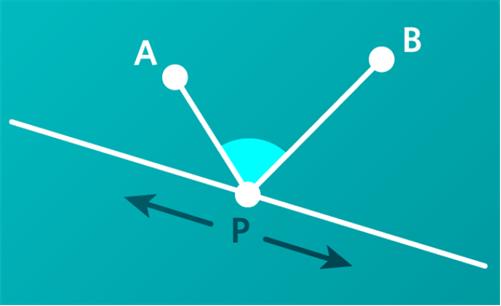 Here is a familiar
Here is a familiar  An excellent application of the solution to this puzzle can be found at
An excellent application of the solution to this puzzle can be found at 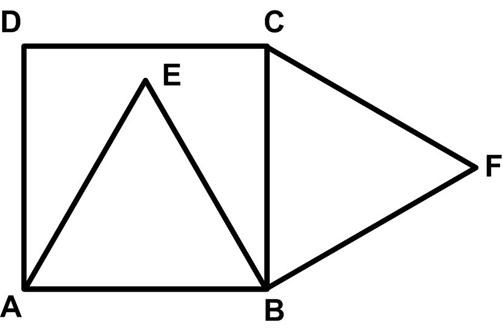 This is a fairly simple problem from
This is a fairly simple problem from  This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.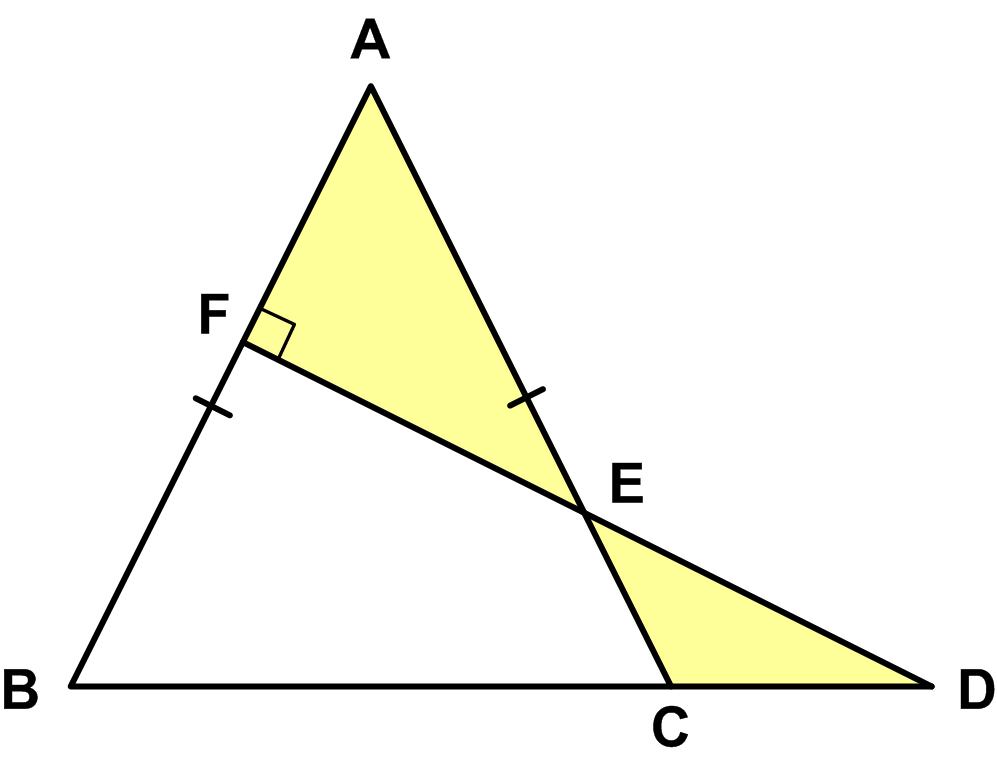 I found this problem from the 1981 Canadian Math Society’s magazine, Crux Mathematicorum, to be quite challenging.
I found this problem from the 1981 Canadian Math Society’s magazine, Crux Mathematicorum, to be quite challenging. Here is another Quantum math magazine Brainteaser.
Here is another Quantum math magazine Brainteaser.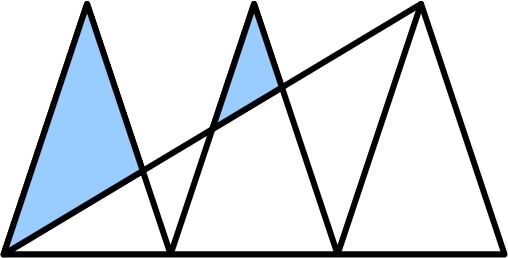 This is a nice little puzzle from the late Nick Berry’s Datagenetics Blog.
This is a nice little puzzle from the late Nick Berry’s Datagenetics Blog.