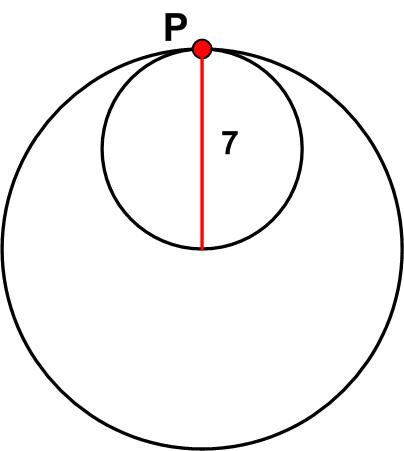
 Here is an intriguing problem from the 2021 Math Calendar.
Here is an intriguing problem from the 2021 Math Calendar.
“If the smaller circle of diameter 7 rotates without slipping within the larger circle, what is the length of the path of P?”
The problem did not state clearly how far the smaller circle should rotate. Its answer implied it should complete just one full (360°) rotation within the larger circle.
Recall that all the answers are integer days of the month.
Answer.
See the Wandering Epicycle for a solution.
(Update 1/3/2022) First, this problem is dealt with in more detail and more expansively on the Mathologer Youtube website by Burkard Polster in his 7 December 2018 post on the “Secrets of the Nothing Grinder” (Figure 1). A further, deeper discussion of epicycles is given in the Mathologer’s 6 July 2018 post on “Epicycles, complex Fourier and Homer Simpson’s orbit” (Figure 2). And finally, a panoply of related puzzles is given in the 30 December 2021 Mathologer post “The 3-4-7 miracle. Why is this one not super famous” (Figure 3).

This last post reveals the ambiguity of the idea of “one full (360°) rotation” I disingenuously added to the problem to try to get the answer given in Math Calendar version.
For a complete explanation see the Wandering Epicycle Addendum.
 Here is another problem from the Polish Mathematical Olympiads published in 1960.
Here is another problem from the Polish Mathematical Olympiads published in 1960.
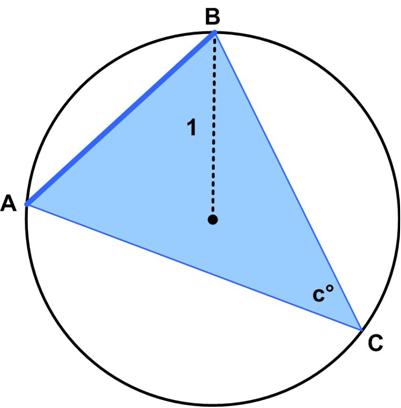 This is another nice puzzle from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.
This is another nice puzzle from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.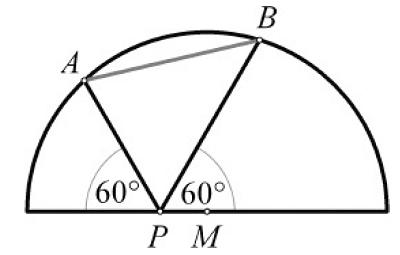 This is an interesting problem from Posamentier and Lehmann’s Mathematical Curiosities.
This is an interesting problem from Posamentier and Lehmann’s Mathematical Curiosities.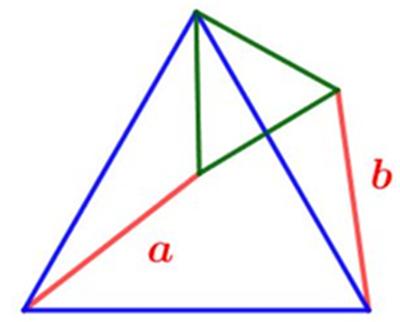 This is another problem from MEI’s MathsMonday.
This is another problem from MEI’s MathsMonday. Here is an intriguing problem from the 2021 Math Calendar.
Here is an intriguing problem from the 2021 Math Calendar.
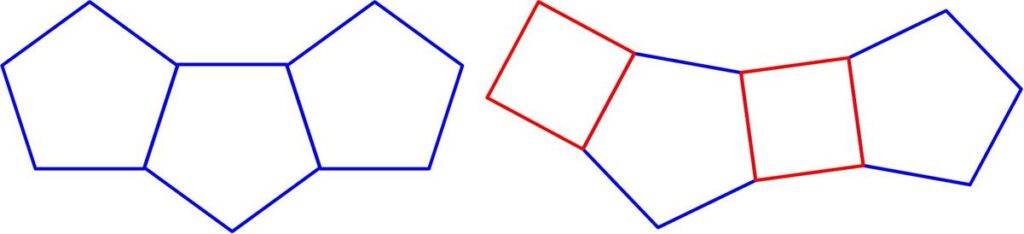 This is a nice geometric problem from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.
This is a nice geometric problem from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.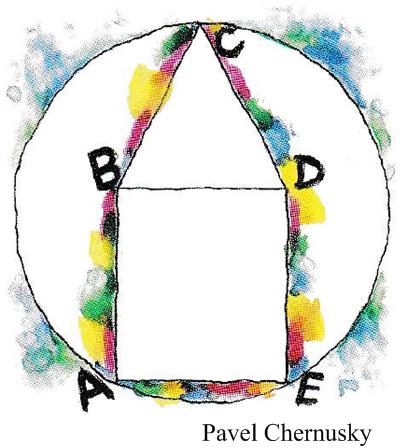 Here is another problem from the “Brainteasers” section of the Quantum magazine.
Here is another problem from the “Brainteasers” section of the Quantum magazine.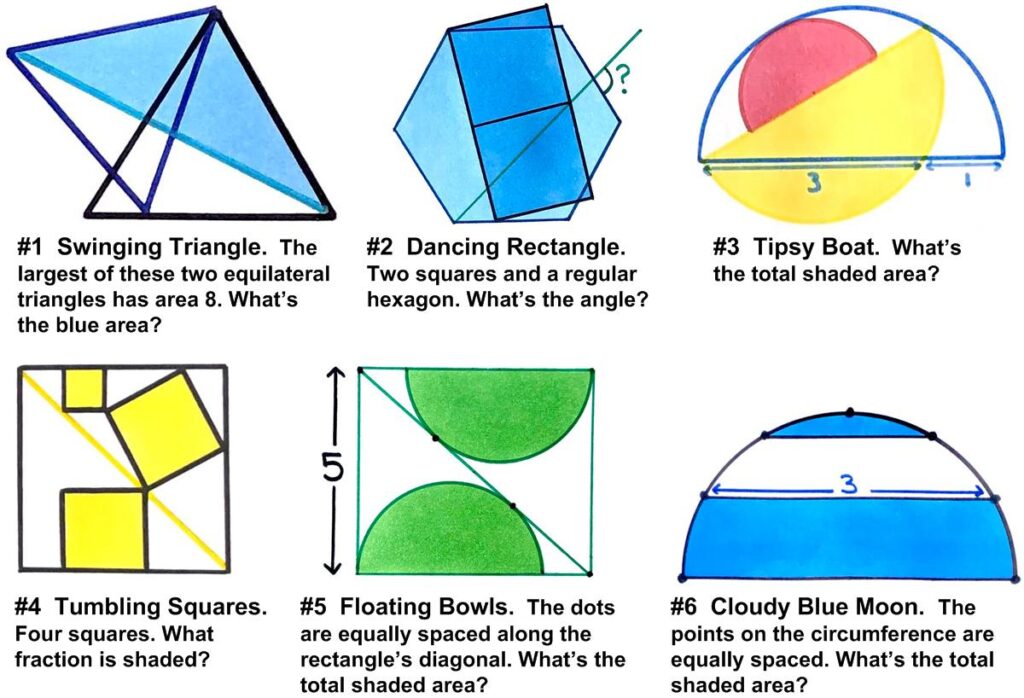 Here is yet another collection of beautiful, stimulating geometric problems from Catriona Agg (née Shearer).
Here is yet another collection of beautiful, stimulating geometric problems from Catriona Agg (née Shearer). This is a nice brain tickling problem from
This is a nice brain tickling problem from 