 Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this Monday Puzzle from Alex Bellos in March is a timely reminder of the mathematical significance of that country.
Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this Monday Puzzle from Alex Bellos in March is a timely reminder of the mathematical significance of that country.
“Like many of you I’ve hardly been able to think about anything else these past ten days apart from the war in Ukraine. So today’s puzzles are a celebration of Lviv, Ukraine’s western city, which played an important role in the history of 20th century mathematics. During the 1930s, a remarkable group of scholars came up with new ideas, methods and theorems that helped shape the subject for decades.
The Lwów school of mathematics – at that time, the city was in Poland – was a closely-knit circle of Polish mathematicians, including Stefan Banach, Stanisław Ulam and Hugo Steinhaus, who made important contributions to areas including set-theory, topology and analysis. …
Of the many ideas introduced by the Lwów school, one of the best known is the “ham sandwich theorem,” posed by Steinhaus and solved by Banach using a result of Ulam’s. It states that it is possible to slice a ham sandwich in two with a single slice that cuts each slice of bread and the ham into two equal sizes, whatever the size and positions of the bread and the ham.
Today’s puzzles are also about dividing food. The first is from Hugo Steinhaus’ One Hundred Problems in Elementary Mathematics, published in 1938. The second uses a method involved in the proof of the ham sandwich theorem.
- Three friends each contribute £4 to buy a £12 ham. The first friend divides it into three parts, asserting the weights are equal. The second friend, distrustful of the first, reweighs the pieces and judges them to be worth £3, £4 and £5. The third, distrustful of them both, weighs the ham on their own scales, getting another result. If each friend insists that their weighings are correct, how can they share the pieces (without cutting them anew) in such a way that each of them would have to admit they got at least £4 of ham?_
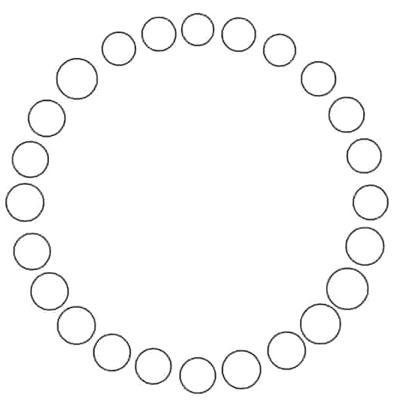
- Ten plain and 14 seeded rolls are randomly arranged in a circle, equidistantly spaced, as below. Show that using a straight line it is possible to divide the circle into two halves such that there are an equal number of plain and seeded rolls on either side of the line.
Show there is always a diameter that cuts the circle into two batches of 12 rolls with an equal number of plain and seeded.
Question 2 is adapted from Mathematical Puzzles by Peter Winkler, who gives as a reference Alon and West, The Borsuk-Ulam Theorem and bisection of necklaces, Proceedings of the American Mathematical Society 98 (1986).”
See The Maths of Lviv
 This seemingly impossible problem from Presh Talwalkar turned out to be quite solvable upon reflection.
This seemingly impossible problem from Presh Talwalkar turned out to be quite solvable upon reflection.
 This is a fun problem from the 1989 American Invitational Mathematics Exam (AIME).
This is a fun problem from the 1989 American Invitational Mathematics Exam (AIME). This puzzle from the Scottish Mathematical Council (SMC) Middle Mathematics Challenge has an interesting twist to it.
This puzzle from the Scottish Mathematical Council (SMC) Middle Mathematics Challenge has an interesting twist to it.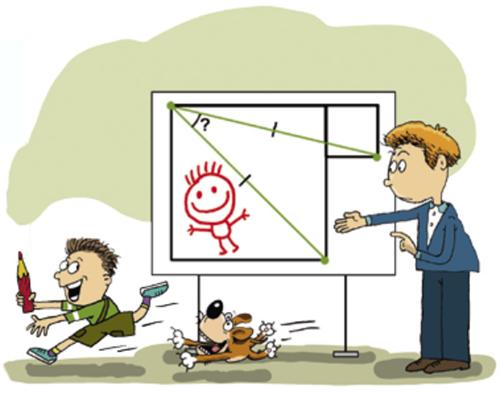 Via Alex Bellos I found another Russian math magazine with fun problems. It is called Kvantik and
Via Alex Bellos I found another Russian math magazine with fun problems. It is called Kvantik and 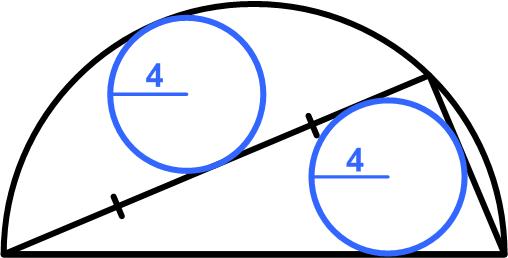 Here is a problem from the 2022 Math Calendar.
Here is a problem from the 2022 Math Calendar. Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this
Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this 
 I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age. I had read an
I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age. I had read an 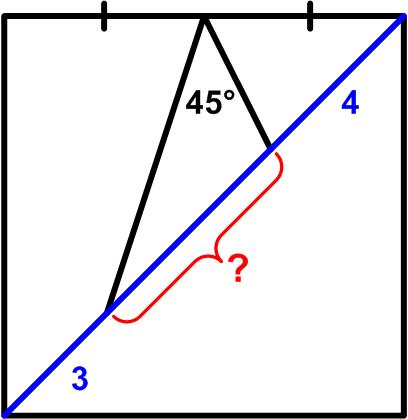 Henk Reuling posted a deceptively simple-looking geometric
Henk Reuling posted a deceptively simple-looking geometric  This
This  As I am sure is common with most mathematicians, I had become interested in the history of the development of mathematical symbols, first for numbers (numerals) and then for algebra (symbolic algebra). Joseph Mazur’s book Enlightening Symbols provided an excellent history of this evolution. His focus on the development and significance of symbolic algebra in the Renaissance was especially illuminating. I also augmented Mazur’s information with details from Albrecht Heeffer’s work.
As I am sure is common with most mathematicians, I had become interested in the history of the development of mathematical symbols, first for numbers (numerals) and then for algebra (symbolic algebra). Joseph Mazur’s book Enlightening Symbols provided an excellent history of this evolution. His focus on the development and significance of symbolic algebra in the Renaissance was especially illuminating. I also augmented Mazur’s information with details from Albrecht Heeffer’s work.