 This is the second part of the problem from Raymond Smullyan in the “Brain Bogglers” section of the 1996 Discover magazine.
This is the second part of the problem from Raymond Smullyan in the “Brain Bogglers” section of the 1996 Discover magazine.
“On another occasion, Al made a mixture of water and wine. There was more water than wine—in fact, the excess of water over wine was equal to one-fourth the quantity of wine. Al then added 12 ounces of wine, at which point there was one ounce more of wine than water.
According to another version of the story, before Al added the 12 ounces of wine, he first boiled off 12 ounces of water (the net effect being that he replaced 12 ounces of water with wine), and again there was one more ounce of wine than water.
Would there be more mixture present at the end of the first version or the second?”
I found this statement a tad ambiguous with the result that I found two possible solutions: the one Smullyan gave and another, surprising one.

 This is a relatively simple problem from the inventive Raymond Smullyan in the “Brain Bogglers” section of the 1996 Discover magazine.
This is a relatively simple problem from the inventive Raymond Smullyan in the “Brain Bogglers” section of the 1996 Discover magazine. This is a nice variation on a racing problem by Geoffrey Mott-Smith from 1954.
This is a nice variation on a racing problem by Geoffrey Mott-Smith from 1954. The June 2023
The June 2023 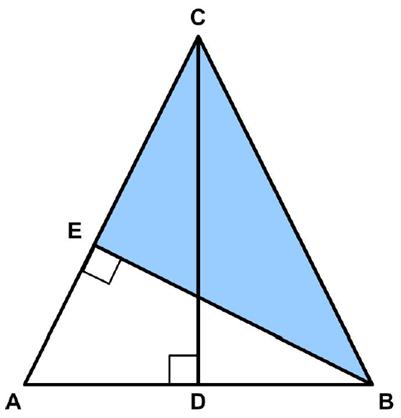 The Futility Closet website had the following
The Futility Closet website had the following 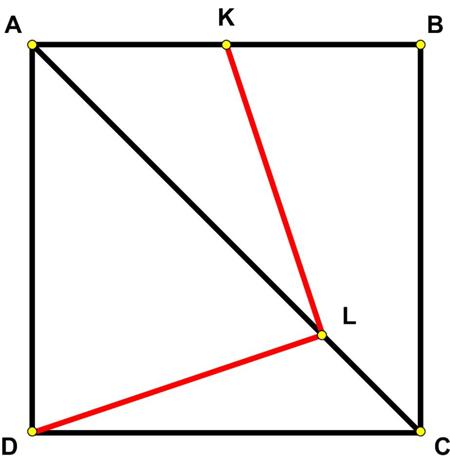 Here is another problem from the “Challenges” section of the Quantum magazine.
Here is another problem from the “Challenges” section of the Quantum magazine. This is a classic example of a mixture problem from Dan Griller that recalls my agonies of beginning algebra.
This is a classic example of a mixture problem from Dan Griller that recalls my agonies of beginning algebra. This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.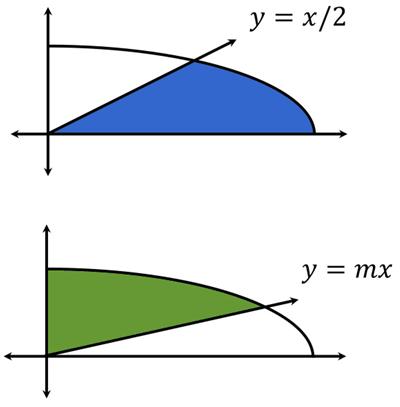 This is a nifty
This is a nifty  One of the physics blogs I enjoy reading is by the mathematical physicist Peter Woit, called
One of the physics blogs I enjoy reading is by the mathematical physicist Peter Woit, called