Henk Reuling posted a deceptively simple-looking geometric problem on Twitter.
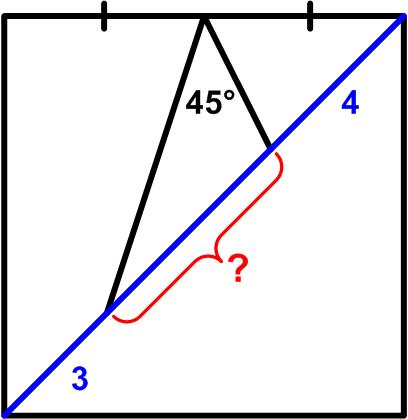
“I found this old one cleaning up my ‘downloads’ [source unknown] I haven’t been able to solve it, so help!
According to the given information in the figure, what is the length of the missing interval on the diagonal of the square?”
See the Missing Interval Puzzle for solutions.
Another solution.
Consider the square as ABCD clockwise with A at top left corner. E is the midpoint of the side AB. F and G are two points on DB such that F is near D and G is near B. DF=3 and BG=4.
************************************
With no construction and using Coordinate Geometry.
Let the B be the origin (0,0) and BE=EA=a= half side of the square.
BG=4 gives G as ( -4/sqrt(2) , -4/sqrt(2) )
DF=3 gives F as ( 2*a – 3/sqrt(2) , 2*a – 3/sqrt(2) ) )
E as ( -a , 0)
If we use k as 1/sqrt(2) in above for ease of typing and understanding,
G is (-4*k, -4*k) and F is (2*a-3*k, 2*a-3*k )
Slope of line EG = [ 0 – (-4*k) ] / [ (-a) – (-4*k)] = m1 say.
Slope of line EF = [ 0 – (2*a-3*k)] / [ -a – (2*a-3*k)] = m2 say.
Since the angle between EG and EF is 45 degrees
tan(45) = (m1 – m2) / ( 1 + m1*m2) = 1
Substituting above and simplifying,
3*a^2 – 22*k*a +24*k^2 = 0
Substituting k= 1/sqrt(2)
3*a^2 – 11*sqrt(2)*a +12 = 0
Solving we get, a = 3*sqrt(2) or (2/3)*sqrt(2)
Valid value is a= 3*sqrt(2)
Diagonal BD^2 = 2*(2*a)^2 = 144 or BD=12
It gives the middle portion as 12-4-3=5 unit.
****************************************
Correcting your coordinates for F to (–2*a + 3*k, –2*a + 3*k ) and thus correcting the slope of EF = m2 to [0 – (–2*a + 3*k)] / [–a – (–2*a + 3*k)], I get your equation 3*a^2 – 22*k*a + 24*k^2 = 0. So good job, especially with some hairy arithmetic. It also required some thinking about the meaning of slopes with respect to tangents.