Via Alex Bellos I found another Russian math magazine with fun problems.  It is called Kvantik and Tanya Khovanova has a description (2015):

“Kvant [Quantum] was a very popular science magazine in Soviet Russia. It was targeted to high-school children and I was a subscriber. Recently I discovered that a new magazine appeared in Russia. It is called Kvantik, which means Little Kvant. It is a science magazine for middle-school children. The previous years’ archives are available online in Russian. I looked at 2012, the first publication year, and loved it.”

Unfortunately, the magazine is in Russian and the later issues are only partially given online.  To get the full magazine you need to subscribe.  I used Google Translate and the mathematical context to render the English.   Here is an interesting geometric problem that I would have thought to be quite challenging for middle schoolers.

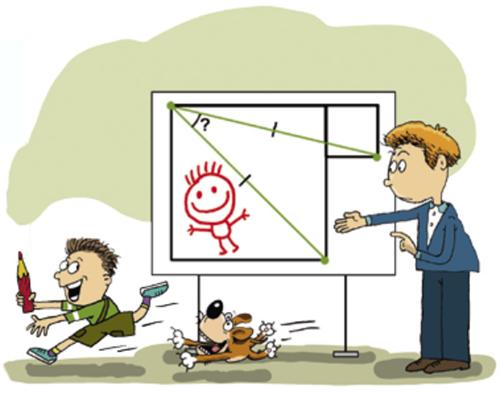
“The vertices of the two squares are joined by two segments, as in the figure. It is given that these segments are equal. Find the angle between them.

Egor Bakaev”

Answer.

See the Two Squares Problem for a solution.

(Update 8/22/2022, 9/1/2022)  Simpler Solution, Simplest Solution!

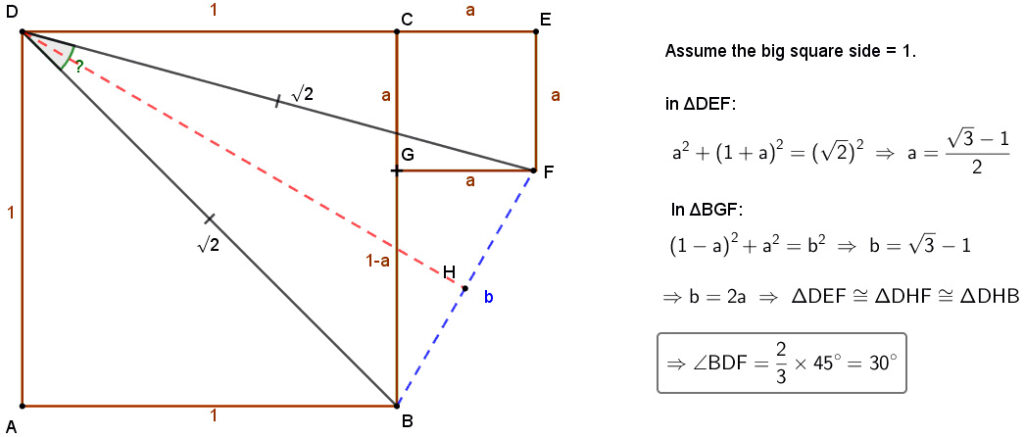
(Update 8/22/2022) Oscar Rojas, a retired IBM systems engineer from Costa Rica, has provided a simpler solution to the problem:

“For the Two-squares-problem my initial approach was to compute the sides and base of the isosceles triangle formed by the two congruent segments, and then apply the Cosine-Law… But a partial result arises with some information that allowed me to take a non-trigonometric shortcut.”

(Update 9/1/2022) Update from Oscar Rojas: “I commented this problem with my friend Ajit Athle from India. He sent this wonderful no-words-needed solution.”

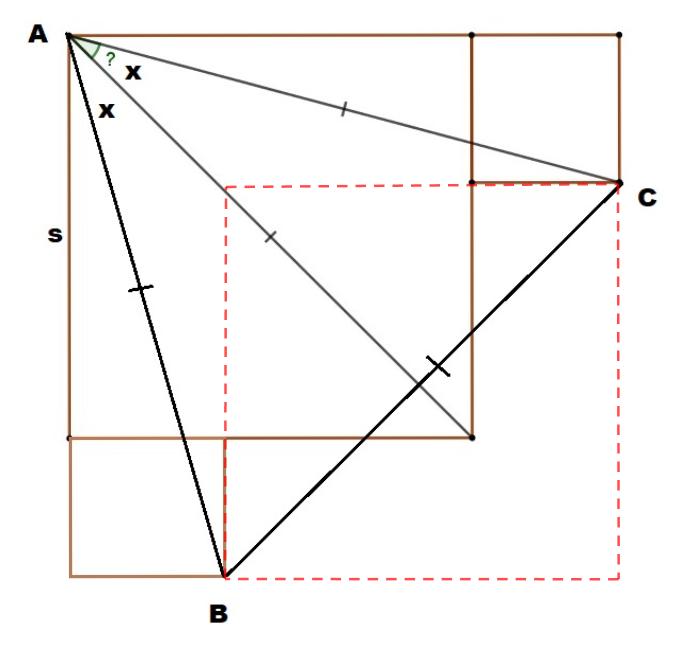
Wow!  This is fantastic!