 This is another long historical story from Sam Loyd with a puzzle attached.
This is another long historical story from Sam Loyd with a puzzle attached.
“NOTICING THE HIGH price recently paid at auction for an autograph of General Grant reminds me to say that I am the proud possessor of what I believe to be the last signature made by General Grant.
The story connected with it introduces a somewhat pretty problem, and induces me to pay a tribute to Grant’s mathematical ability, at the expense of the many who have no love for figures. I take occasion here to say that while journeying through life and jostling up against all manner of people, the fact has been impressed upon my mind that with few exceptions all successful men were those who endowed with a ready faculty for correct mental arithmetic. On the other hand, there is a class of never-do-wells who guess or jump at conclusions in a reckless way, and cannot even figure up how much to pay on the dollar when the inevitable smash comes.
I could mention a dozen incidents connected with great men as illustrating their aptitude for correct calculations, but this one will suffice to call attention to Grant’s aptitude for figures.
We all remember the story of how he figured his way into West Point, after that memorable journey for a pound of butter, when he heard of the chance for a competitive examination. Professor Agnell, the master of mathematics at West Point, with whom I used to play chess, used to say that “Grant had a great love for mathematics and horses.”
Grant did love a horse and could pick out the good qualities at a glance, and, oh, my! how he despised a man who would abuse a dumb animal!
My story turns upon an incident as told by Ike Reed, of the old horse mart of Johnson & Reed, who gave me the autograph from their sales book of 1884, as photographed in the picture. During the last term of his Presidency General Grant returned from his afternoon drive and in a humorous but somewhat mortified way told Colonel Shadwick, who kept the Willard Hotel, that he had been passed on the road by a butcher cart in a way that made his crack team appear to be standing still. He said he would like to know who owned the horse and if it was for sale.
The horse was readily found and purchased from an unsophisticated German for half of what he would have asked had he known the purchaser was the President of the United States. The horse was of light color and was none other than Grant’s favorite horse, “Butcher Boy,” named after the incident mentioned. Well, some years later, after the Wall street catastrophe, which impaired the finances of the Grant family, Butcher Boy and his mate were sent to the auction rooms of Johnson & Reed, and sold for the sum of $493.68. Mr. Reed said he could have gotten twice as much for them if he had been permitted to mention their ownership. But General Grant positively prohibited the fact being made known. “Nevertheless,” said Reed. “you come out two per cent, ahead, for you make 12 per cent, on Butcher Boy and lose 10 per cent, on the other.”
“I suppose that is the way some people would figure it out.” replied the General, but the way he laughed showed that he was better at figures than some people, so I am going to ask our puzzlists to tell me what he got for each horse if he lost 10 per cent on one and made 12 per cent on the other, but cleared 2 per cent on the whole transaction?
It may be mentioned incidentally that General Grant stated that he had presented one of the horses to Mrs. Fred Grant, and as shown in the receipt signed for her.”
Answer.
See the Butcher Boy Problem for solution.
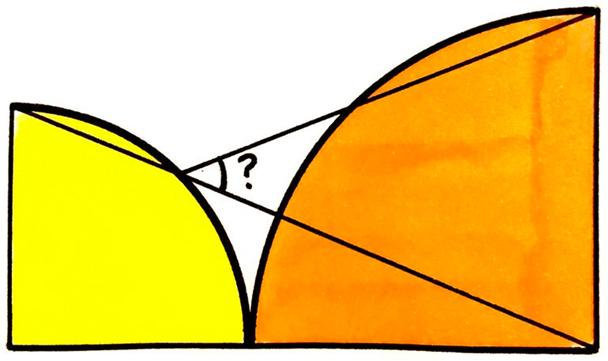 This is a Catriona Agg problem presented by itself, since it turned out to be the most challenging one I ever tried. Usually I can solve her problems in a few minutes or maybe hours, or sometimes days if they are especially challenging. But this problem has taken me weeks and I had to rely on a non-geometric argument. The problem is full of fascinating and unexpected relationships, but I couldn’t find a way to use them to prove the answer.
This is a Catriona Agg problem presented by itself, since it turned out to be the most challenging one I ever tried. Usually I can solve her problems in a few minutes or maybe hours, or sometimes days if they are especially challenging. But this problem has taken me weeks and I had to rely on a non-geometric argument. The problem is full of fascinating and unexpected relationships, but I couldn’t find a way to use them to prove the answer.
 Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem.
Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem. This is a straight-forward problem from Five Hundred Mathematical Challenges.
This is a straight-forward problem from Five Hundred Mathematical Challenges. This is a fun problem from the 1949 Eureka magazine.
This is a fun problem from the 1949 Eureka magazine.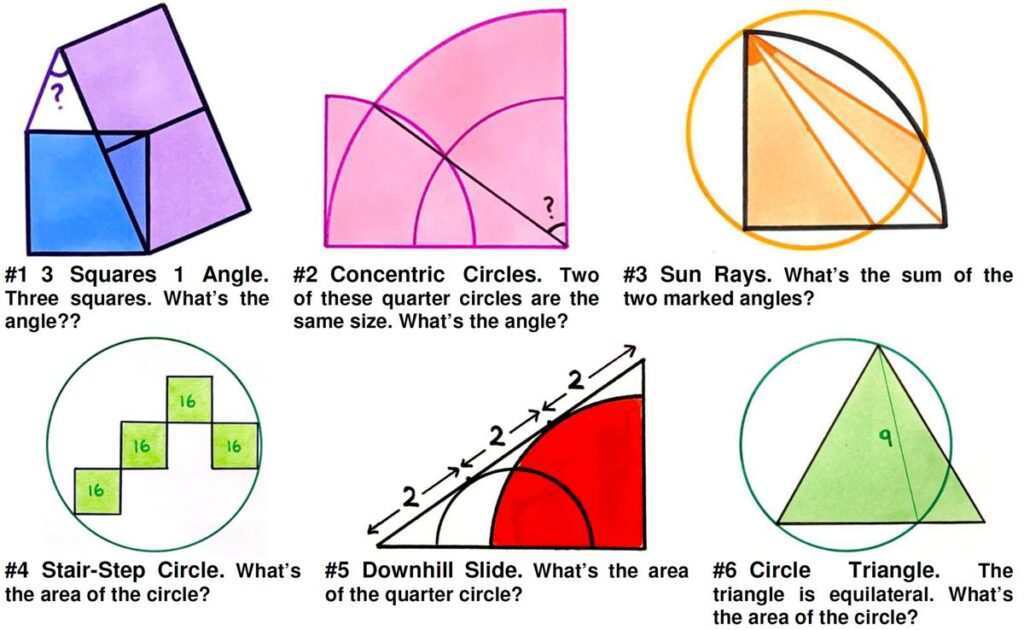 Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer).
Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer).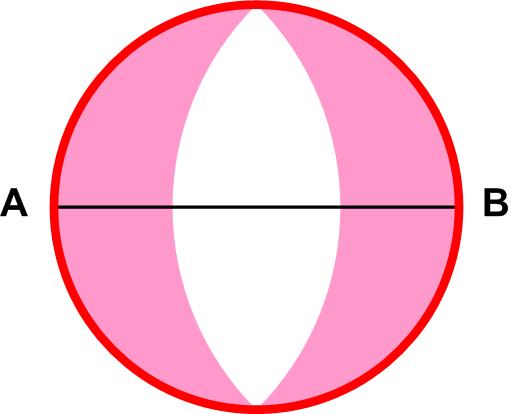 This is a straight-forward problem from the Scottish Mathematical Council (SMC) Senior Mathematics Challenge.
This is a straight-forward problem from the Scottish Mathematical Council (SMC) Senior Mathematics Challenge.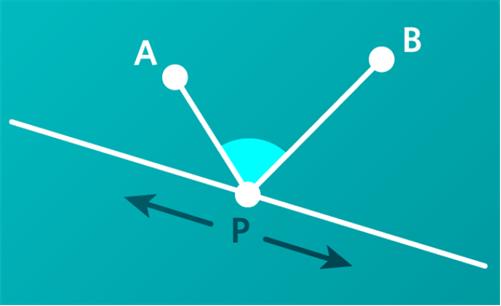 Here is a familiar
Here is a familiar  An excellent application of the solution to this puzzle can be found at
An excellent application of the solution to this puzzle can be found at  This is another long historical story from Sam Loyd with a puzzle attached.
This is another long historical story from Sam Loyd with a puzzle attached.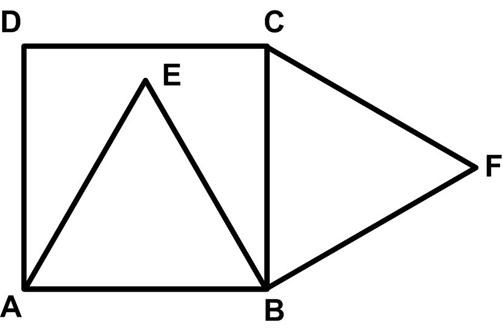 This is a fairly simple problem from
This is a fairly simple problem from  This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.