 One is reduced to hysterical laughter to try to maintain a modicum of sanity.
One is reduced to hysterical laughter to try to maintain a modicum of sanity.
Our Senate at work: Republican Mitch McConnell said (Dec 6) “Legislation that doesn’t include policy changes to secure our borders will not pass the Senate.” Republican Trump said (Feb 3) the Senate should not pass legislation that includes border security. Let P be the statement “Senate legislation should include border security.” and let Q be the statement “Senate should pass legislation.” Then we have the Republicans saying
(~P ⇒ ~Q) ˄ (P ⇒ ~Q)
Show that this is equivalent to ~Q, that is, “The Senate should not pass legislation.”—basically stop working.
It looks like the Republicans in the House are doing the same thing:
See Logical Dead End
Old Codger Rant, with Update (4/24/2024): Continue reading


 This is yet another simple problem from Henry Dudeney.
This is yet another simple problem from Henry Dudeney. Here is a fairly computationally challenging 1994 AIME problem .
Here is a fairly computationally challenging 1994 AIME problem . My cousin sent me this
My cousin sent me this  Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
 So I managed to make it five years. Again, I thought I would present the statistical pattern of interaction with the website in the absence of any explicit feedback.
So I managed to make it five years. Again, I thought I would present the statistical pattern of interaction with the website in the absence of any explicit feedback.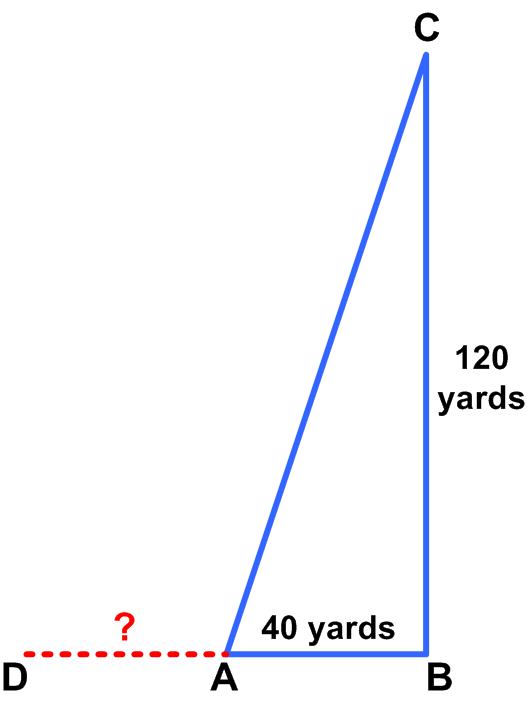 The following puzzle is from the Irishman Owen O’Shea.
The following puzzle is from the Irishman Owen O’Shea.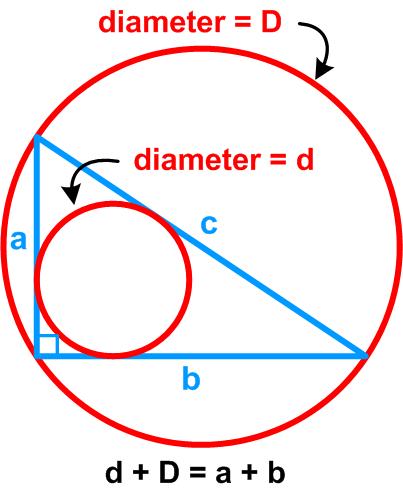
 This is yet another series offered by
This is yet another series offered by 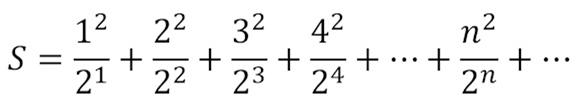
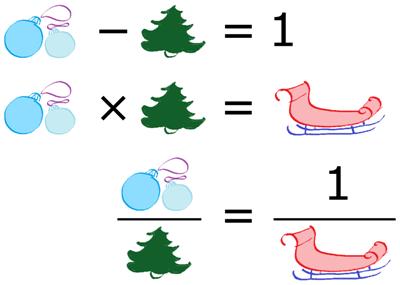 This is a slightly different mystery number puzzle from the December 2023
This is a slightly different mystery number puzzle from the December 2023