 This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.
This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.
“In a 100 meter race, Jacob can beat Johann by 5 meters, and Johann can beat Nicolaus by 10 meters. By how much can Jacob beat Nicolaus?”
See Yet Another Race for a solution.

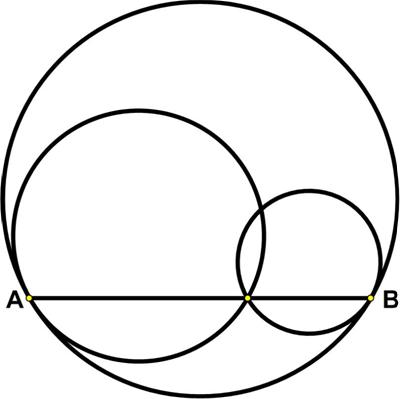 Here is another problem from the “Challenges” section of the Quantum magazine.
Here is another problem from the “Challenges” section of the Quantum magazine.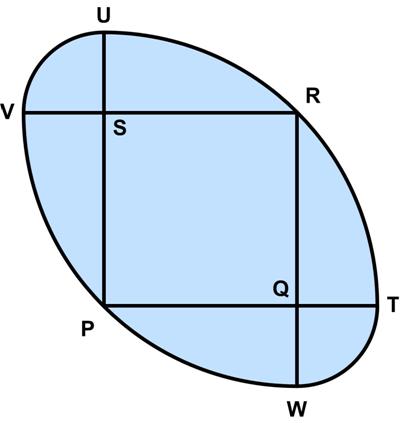 Here is another UKMT Senior Challenge problem for 2017.
Here is another UKMT Senior Challenge problem for 2017.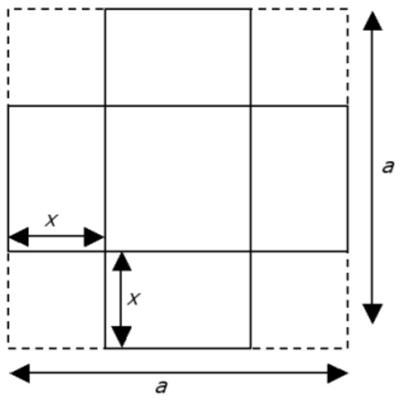 This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net). Here is another classic example of the three jug problem posed in the Mathigon Puzzle Calendars for 2017.
Here is another classic example of the three jug problem posed in the Mathigon Puzzle Calendars for 2017. This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.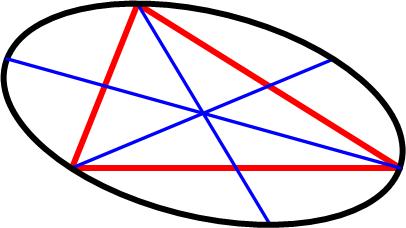 This is a tantalizing problem from the 1977 Crux Mathematicorum.
This is a tantalizing problem from the 1977 Crux Mathematicorum. This is a somewhat challenging problem from the 1997 American Invitational Mathematics Exam (AIME).
This is a somewhat challenging problem from the 1997 American Invitational Mathematics Exam (AIME). This is a nifty
This is a nifty  This is a fairly extensive clock problem by Geoffrey Mott-Smith from 1954.
This is a fairly extensive clock problem by Geoffrey Mott-Smith from 1954.