 This is a Maths Item of the Month (MIOM) problem that seems opaque at first. (“The Maths Item of the Month is a monthly problem aimed at teachers and students of GCSE and A level Mathematics.”)
This is a Maths Item of the Month (MIOM) problem that seems opaque at first. (“The Maths Item of the Month is a monthly problem aimed at teachers and students of GCSE and A level Mathematics.”)
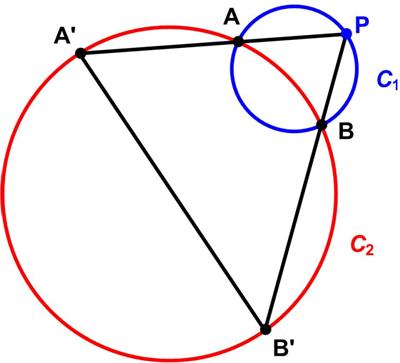
“Two fixed circles, C1 and C2, intersect at A and B. P is on C1. PA and PB produced meet C2 at A’ and B’ respectively. How does the length of the chord A’B’ change as P moves?”
Just start noticing relationships and the answer falls out nicely.
(MIOM problems often appear on MathsMonday and are also produced by Mathematics Education Innovation (MEI).)
See the Triangle Projection Problem for a solution.

WordPress in their infinite wisdom decided to arbitrarily change the heading format for some reason. They also made sure there was no way to change it back, as far as I could tell, thus compounding a long list of poor user interface practices they have employed. One more reason I hate to format articles online. A lot of us just want a simple posting option with some basic capabilities. WordPress does offer a number of useful capabilities, as well as an option to write your own HTML. But they have a large number of infelicities. I attempted to navigate their “help” areas and that was a labyrinthine nightmare with many skeletons of ignored requests for help. So I apologize for some ugliness creeping into the postings.
(Update 12/31/2022) I finally figured out a way to remove the bold face.
No equations needed, just observations:
On C1, by inscribed angle theorem, measure of angle APB is constant, no matter the position of P.
On C2, by converse of outside angle theorem, measure of arc A’B’ is constant, as well as the length of chord A’B’.
Nice observation. I am afraid I don’t remember an “outside angle theorem”. I will have to look that up. Thanks.