 Here is yet another collection of beautiful, stimulating geometric problems from Catriona Agg (née Shearer).
Here is yet another collection of beautiful, stimulating geometric problems from Catriona Agg (née Shearer).
Tag Archives: plane geometry
Two Curious Semicircles
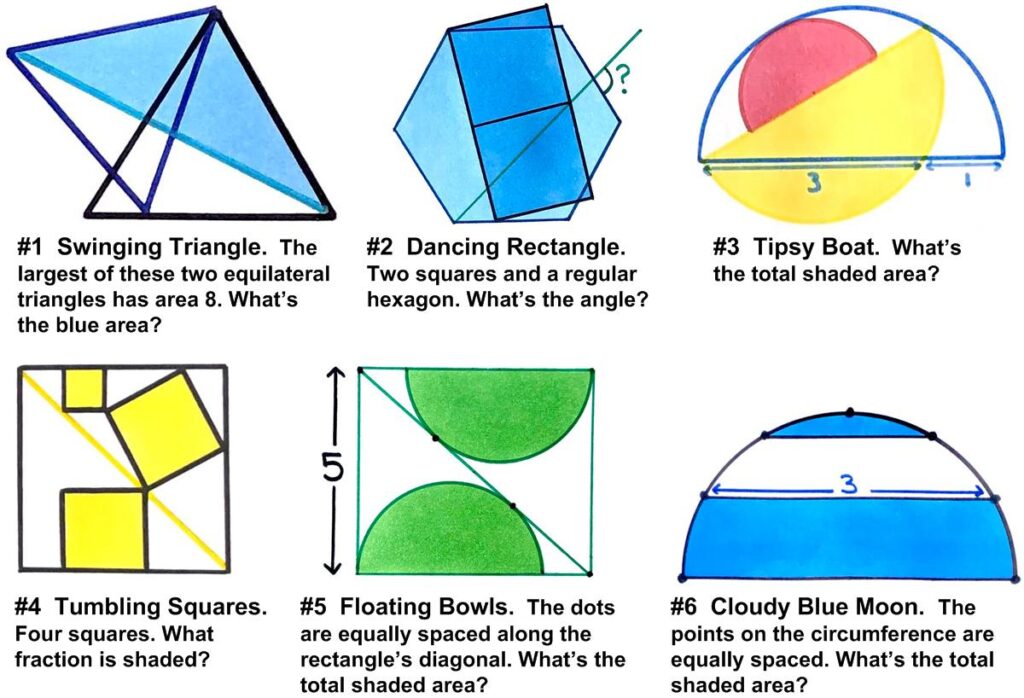
 This is a nice brain tickling problem from Presh Talwalkar.
This is a nice brain tickling problem from Presh Talwalkar.
“A circle contains two tangent semicircles whose diameters are parallel chords. If the circle has an area equal to 1, what is the combined area of the two semicircles?”
See the Two Curious Semicircles for solutions.
Topple Blocks Puzzle

This is another imaginative puzzle from MEI’s MathsMonday. I didn’t know what topple blocks were at first, but a previous MathsMonday puzzle defined them as shown in the first frame. Apparently they derive from the game of Jenga created by Leslie Scott and launched in 1983.
See the Topple Blocks Puzzle
Triangle Quadrangle Puzzle
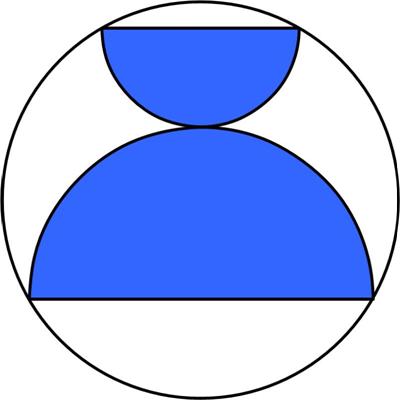
 This is another simple problem from Five Hundred Mathematical Challenges:
This is another simple problem from Five Hundred Mathematical Challenges:
“Problem 57. Let X be any point between B and C on the side BC of the convex quadrilateral ABCD (as in the Figure). A line is drawn through B parallel to AX and another line is drawn through C parallel to DX. These two lines intersect at P. Prove that the area of the triangle APD is equal to the area of the quadrilateral ABCD.”
See the Triangle Quadrangle Puzzle
Bottema’s Theorem
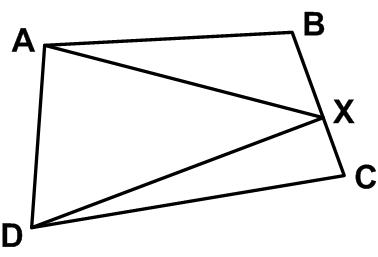
This seemingly magical result from Futility Closet defies proof at first. Go to the Wolfram demo by Jay Warendorff and then …
“Grab point B above and drag it to a new location. Surprisingly, M, the midpoint of RS, doesn’t move.
This works for any triangle — draw squares on two of its sides, note their common vertex, and draw a line that connects the vertices of the respective squares that lie opposite that point. Now changing the location of the common vertex does not change the location of the midpoint of the line.
It was discovered by Dutch mathematician Oene Bottema.”
As we shall see, Bottema’s Theorem has shown up in other guises as well.
Snooker Puzzle
 This is a nice puzzle from Alex Bellos’s Monday Puzzle column in the Guardian.
This is a nice puzzle from Alex Bellos’s Monday Puzzle column in the Guardian.
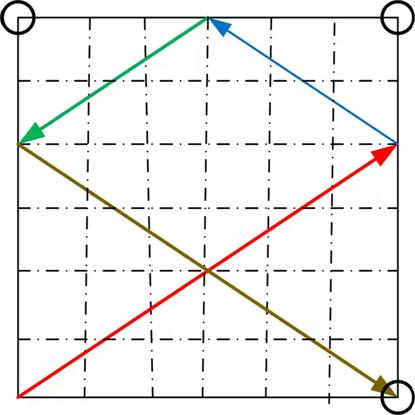
“My cultural highlight of recent weeks has been the brilliant BBC documentary Gods of Snooker, about the time in the 1980s when the sport was a national obsession. Today’s puzzle describes a shot to malfunction the Romford Robot … and put the Whirlwind … in a spin.
Baize theorem
A square snooker table has three corner pockets, as [shown]. A ball is placed at the remaining corner (bottom left). Show that there is no way you can hit the ball so that it returns to its starting position.
The arrows represent one possible shot and how it would rebound around the table.
The table is a mathematical one, which means friction, damping, spin and napping do not exist. In other words, when the ball is hit, it moves in a straight line. The ball changes direction when it bounces off a cushion, with the outgoing angle equal to the incoming angle. The ball and the pockets are infinitely small (i.e. are points), and the ball does not lose momentum, so that its path can include any number of cushion bounces.
Thanks to Dr Pierre Chardaire, associate professor of computing science at the University of East Anglia, who devised today’s puzzle.”
See the Snooker Puzzle
Area vs. Perimeter Puzzle
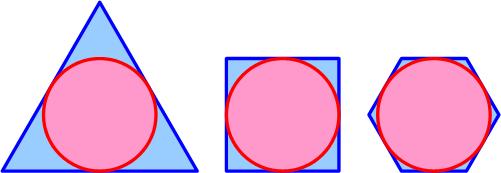 This surprising, but simple, puzzle is from the 12 April MathsMonday offering by MEI, an independent curriculum development body for mathematics education in the UK.
This surprising, but simple, puzzle is from the 12 April MathsMonday offering by MEI, an independent curriculum development body for mathematics education in the UK.
“In the diagram various regular polygons, P, have been drawn whose sides are tangents to a circle, C. Show that for any regular polygon drawn in this way:”
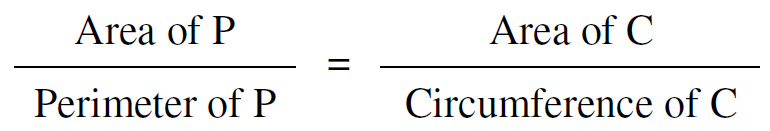
(Given that the polygons approximate the circle in the limit, it would not be surprising that this relationship would hold—in the limit. It is surprising that it should be true for every regular polygon that circumscribes the circle.)
See the Area vs. Perimeter Puzzle
Center of Square Problem
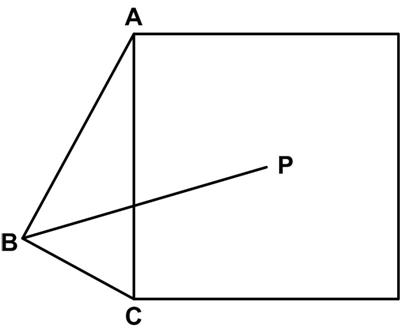 This is a simple problem from Five Hundred Mathematical Challenges:
This is a simple problem from Five Hundred Mathematical Challenges:
“Problem 24. Let P be the center of the square constructed on the hypotenuse AC of the right-angled triangle ABC. Prove that BP bisects angle ABC.”
See the Center of Square Problem
Geometric Puzzle Magnificence
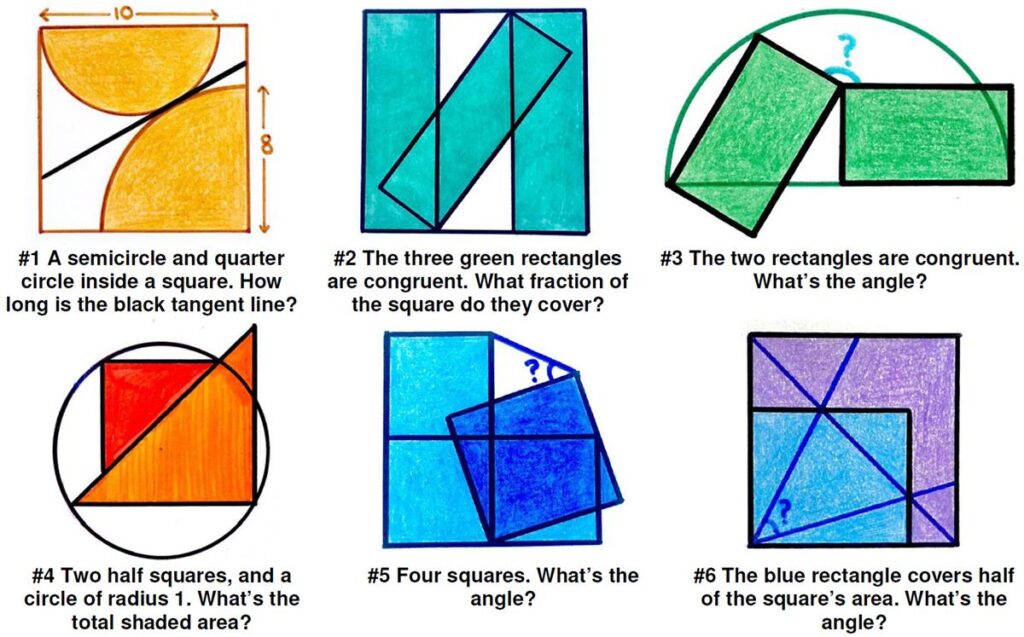 Here is yet another collection of beautiful geometric problems from Catriona Agg (née Shearer). For some reason I found these a bit more challenging than the previous ones. Some of them required more time to “see” the breakthrough.
Here is yet another collection of beautiful geometric problems from Catriona Agg (née Shearer). For some reason I found these a bit more challenging than the previous ones. Some of them required more time to “see” the breakthrough.
See Geometric Puzzle Magnificence (revised)
(Update 11/13/2022) Problem #3 Solution Corrected Continue reading
Equitable Slice Problem
 This is another Brainteaser from the Quantum math magazine .
This is another Brainteaser from the Quantum math magazine .
“How can a polygonal line BDEFG be drawn in a triangle ABC so that the five triangles obtained have the same area?”
I found this problem rather challenging, especially when I first tried to solve it analytically (using hyperbolas). Eventually I arrived at a procedure that would accomplish the result. (revised)
See the Equitable Slice Problem (revised)
(Update 9/22/2021) I goofed. I erroneously and foolishly thought Quantum had not solved the problem. Upon a closer reading I see what they were getting at and revised the posting.
