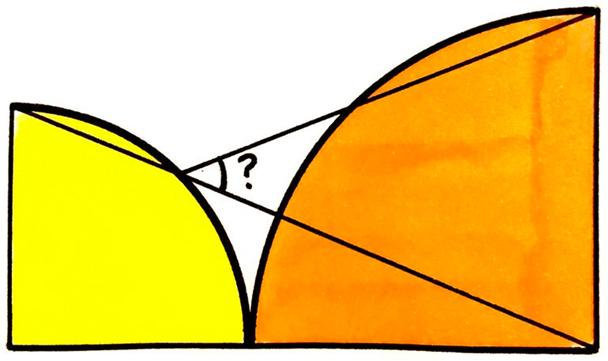
This is a Catriona Agg problem presented by itself, since it turned out to be the most challenging one I ever tried.  Usually I can solve her problems in a few minutes or maybe hours, or sometimes days if they are especially challenging.  But this problem has taken me weeks and I had to rely on a non-geometric argument.  The problem is full of fascinating and unexpected relationships, but I couldn’t find a way to use them to prove the answer.

See the Curious Sunbeam Problem

(Update 5/5/2023)  Alternative Solution

Here is a solution offered by Oscar Rojas (5/1/2023):

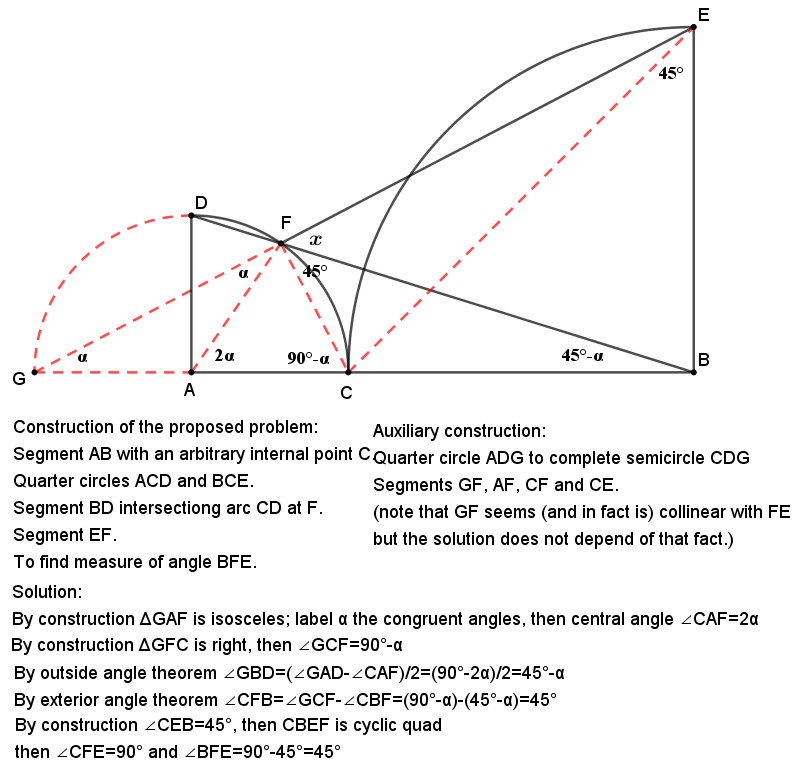
Several people on Catriona Agg’s twitter site mentioned cyclic quadrilaterals, but that is not such a familiar concept to me, other than being a quadrilateral whose vertices all lie on a circle.  I went to Wikipedia to look at properties, of which there are many, and tried to find something that might be relevant.  But I confess I failed, though I did not pursue it too extensively.  My first problem is that it was not obvious to me that the four points B, C, E, and F all lie on a circle.  Sure, any three could, but what about the fourth?  What property explicitly was used to prove they were cyclic? 

Another question I had was regarding the “outside angle theorem”.  I admit I had not heard of that, or if I did, I did not remember it after more than 60 years.  I did a Google search and found many references to the “external angle theorem”, which is obvious and common, but nothing about an “outside angle theorem”.  So it would have been helpful to state it and perhaps give a reference.  But of course I had found the angle was 45° by a different method. 

To have to resort to less elementary geometric properties makes the problem a bit harder, which Catriona admitted, though her approach was even different (and not immediately obvious to me).  Clearly, I am an amateur when it comes to the vast repertoire of plane geometry, which might be expected for anyone regarding a subject that was developed over 2000 years.  I just like how many geometric puzzles one can solve with the simplest ideas.