 This is an interesting problem from Posamentier and Lehmann’s Mathematical Curiosities.
This is an interesting problem from Posamentier and Lehmann’s Mathematical Curiosities.
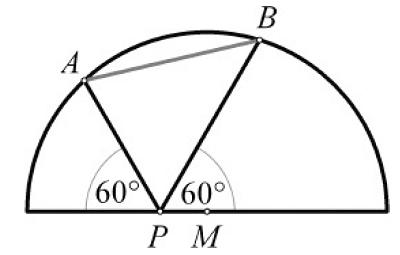
“In the figure we have a semicircle with the point P randomly placed on the diameter. Points A and B are situated on the circle such that they form angles of 60° with the diameter as shown in the figure. This problem asks us to show that the length of AB is equal to the radius of the semicircle.”
See the Ubiquitous Radius Problem
