This is a nice brain tickling problem from Presh Talwalkar.
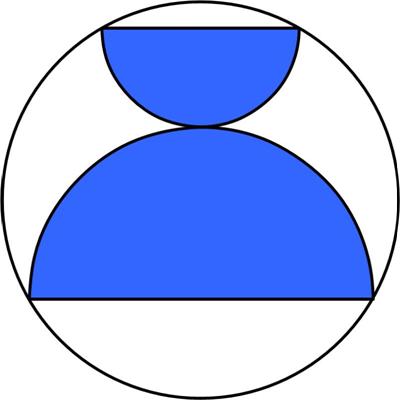
“A circle contains two tangent semicircles whose diameters are parallel chords. If the circle has an area equal to 1, what is the combined area of the two semicircles?”
See the Two Curious Semicircles for solutions.
Sir,
I have found one more simple solution. With reference to your diagram, let the blue segment between the center of the circle and the touching point of the two semicircles be x.
Then ^2 = r^2 + (r+x)^2 and
^2 = R^2 + (R-x)^2
Equating the two RHSs,
r^2 + r^2 + x^2 + 2*r*x = R^2 + R^2 + x^2 – 2*R*x
R^2 – r^2 = x*(R+r)
(R+r)*(R-r) = x*(R+r)
x = R-r
Substituting in first or second equation,
^2 = r^2 + R^2
Rest follows.