 Here is another problem from the Polish Mathematical Olympiads published in 1960.
Here is another problem from the Polish Mathematical Olympiads published in 1960.
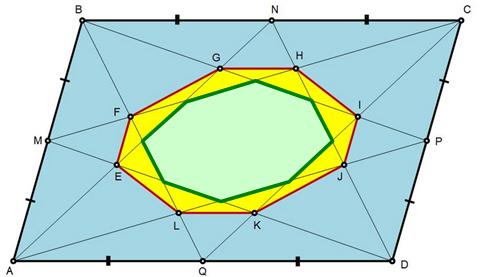
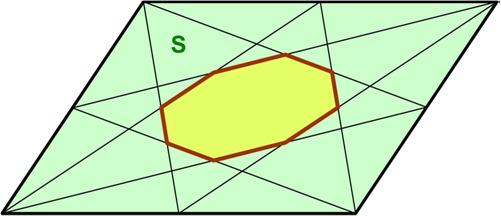
“95. In a parallelogram of given area S each vertex has been connected with the mid-points of the opposite two sides. In this manner the parallelogram has been cut into parts, one of them being an octagon. Find the area of that octagon.”
See the Octagonal Area Problem for solutions.

This was nice and reminded me of Enigma 1313, which appeared in the New Statesman about 20 years ago (and, I think, in Graham’s Dial before that). Also of Marion Walter’s Theorem.
Two thoughts: I had not heard of Marion’s Theorem and so looked it up. There are similarities, but Marion’s Theorem is much more challenging.
Second. It is not surprising that this problem may have appeared elsewhere. There really are only a finite number of basically different types of problems. Some authors of books readily admit their repurposing and may give the genealogy of the problem as far as they can determine it. I make it explicit that I am using others’ problems rather than my own creations. I do try to find them in a wide variety of places and times. The historical problems are especially illuminating, but often a little too computation-heavy for my tastes.
https://gogeometry.com/school-college/5/p1494-parallelogram-midpoints-octagon-area.htm
A similar problem, if not identical, appears on the above website/link. The problem claims the area
of the interior Octagon is 7S/25. (not S/6). What are the differences in the two problems? I am surely missing something in my understanding of the two problem statements.
Thanks very much for the comment. It took me a moment to see the difference between the problems. I have superimposed the octagon in my problem (now green) over the one in Problem 1494. You can see they are different, and the one in my problem is smaller. That at least is in agreement with 1/6 < 7/25.