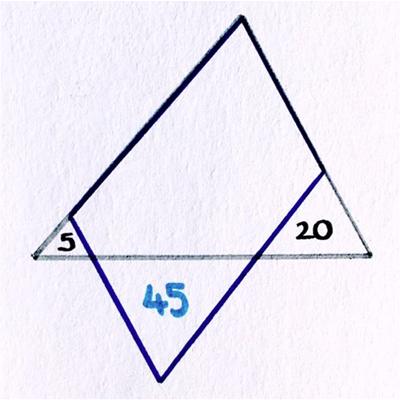
 Catriona Shearer has come up with another challenging but elegant geometric problem. In some ways, it is similar to the famous Russian Coffin Problems that have an obvious solution—once you see it—but initially seem impenetrable. I really marvel at Catriona Shearer’s ability to come up with these problems.
Catriona Shearer has come up with another challenging but elegant geometric problem. In some ways, it is similar to the famous Russian Coffin Problems that have an obvious solution—once you see it—but initially seem impenetrable. I really marvel at Catriona Shearer’s ability to come up with these problems.
“What’s the area of the parallelogram?”
See the Parallelogram Problem for a solution.

 A mathematics friend of mine just sent me this link to a 2017
A mathematics friend of mine just sent me this link to a 2017 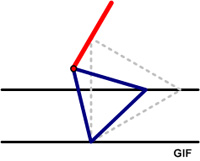
 Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation.
Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation.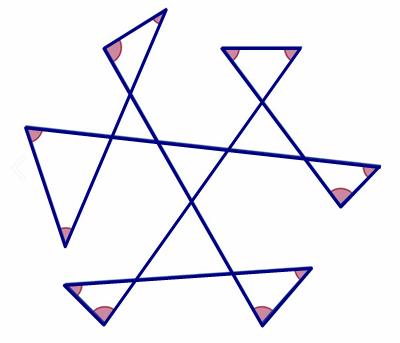
 Setting aside my chagrin that the following problem was given to pre-university students, I initially found the problem to be among the daunting ones that offer little information for a solution. It also was a bit “inelegant” to my way of thinking, since it involved considering some separate cases. Still, the end result turned out to be unique and satisfying (Talwalkar’s Note 2 was essential for a unique solution, since the problem as stated was ambiguous).
Setting aside my chagrin that the following problem was given to pre-university students, I initially found the problem to be among the daunting ones that offer little information for a solution. It also was a bit “inelegant” to my way of thinking, since it involved considering some separate cases. Still, the end result turned out to be unique and satisfying (Talwalkar’s Note 2 was essential for a unique solution, since the problem as stated was ambiguous).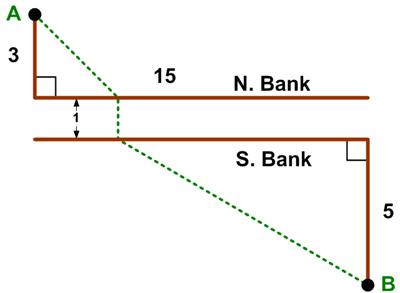 This is a riff on a classic problem, given in Challenging Problems in Algebra.
This is a riff on a classic problem, given in Challenging Problems in Algebra.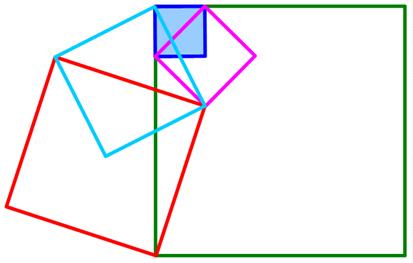 Here is another imaginative geometry problem from
Here is another imaginative geometry problem from 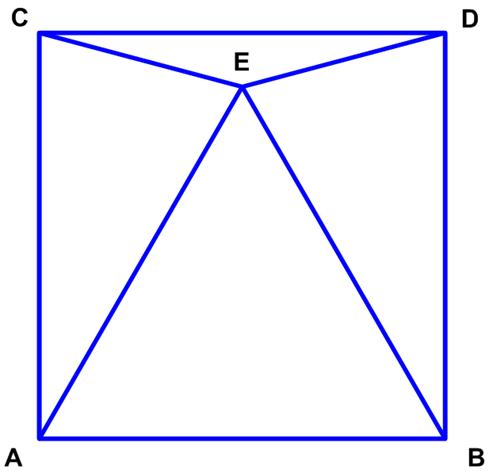 The issue 7 of the Chalkdust mathematics magazine had an interesting geometric problem presented by Matthew Scroggs.
The issue 7 of the Chalkdust mathematics magazine had an interesting geometric problem presented by Matthew Scroggs. It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the
It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the