 This is an interesting problem from the Canadian Mathematical Society’s 2001 Olymon.
This is an interesting problem from the Canadian Mathematical Society’s 2001 Olymon.
“Suppose that XTY is a straight line and that TU and TV are two rays emanating from T for which XTU = UTV = VTY = 60º. Suppose that P, Q and R are respective points on the rays TY, TU and TV for which PQ = PR. Prove that QPR = 60º.”
See the Ubiquitous 60 Degree Problem

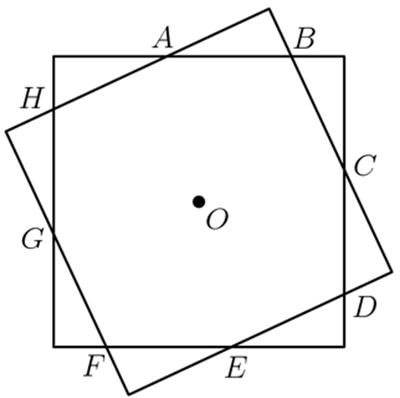 This is a fairly straight-forward problem from the 1999 AIME problems.
This is a fairly straight-forward problem from the 1999 AIME problems.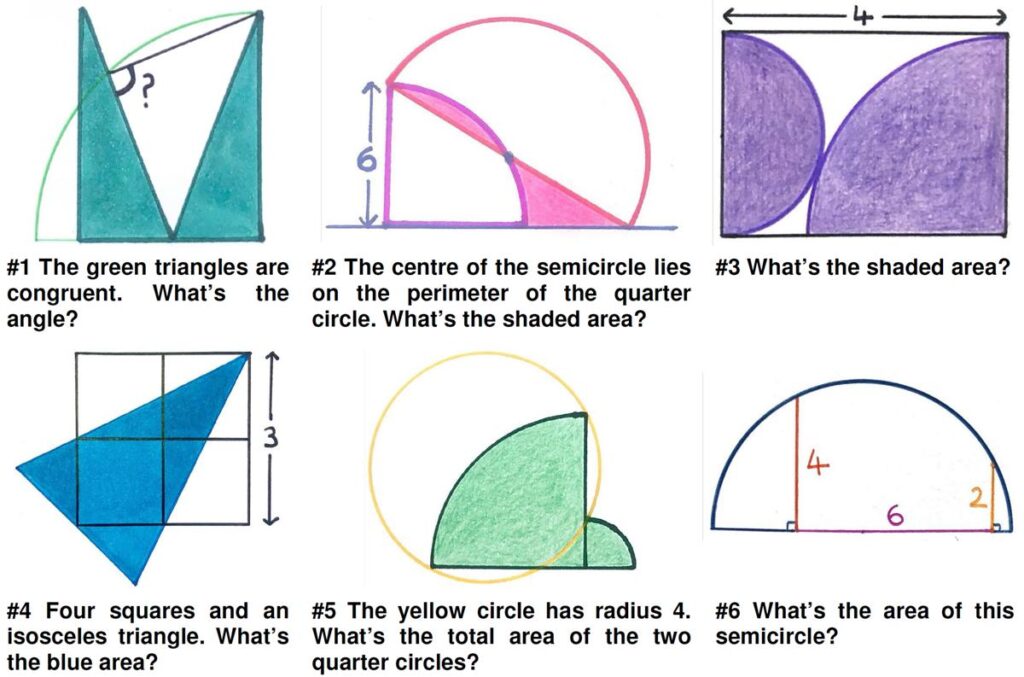
 Coming across this
Coming across this 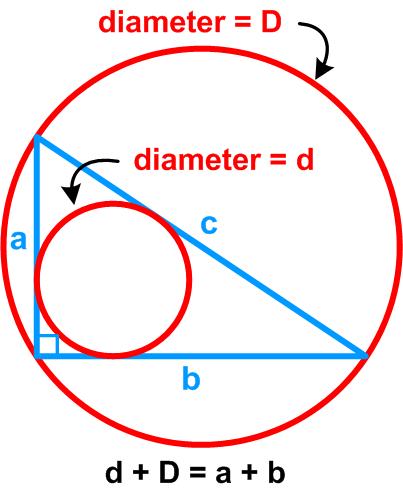
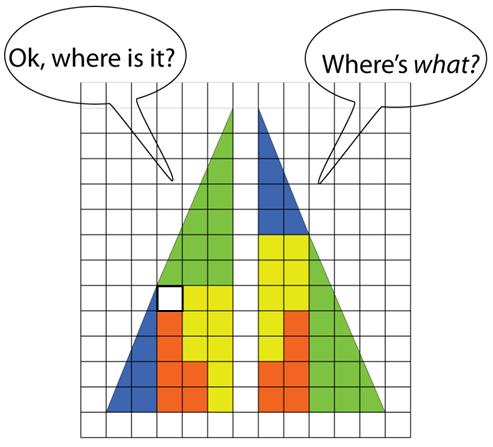
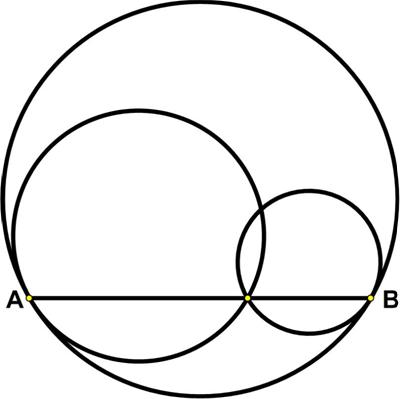 Here is another problem from the “Challenges” section of the Quantum magazine.
Here is another problem from the “Challenges” section of the Quantum magazine.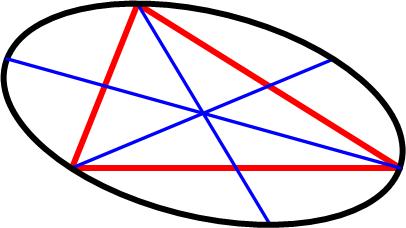 This is a tantalizing problem from the 1977 Crux Mathematicorum.
This is a tantalizing problem from the 1977 Crux Mathematicorum.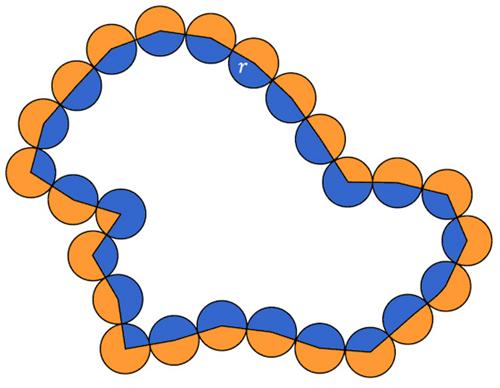 This is a nifty
This is a nifty  This is another puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is another puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.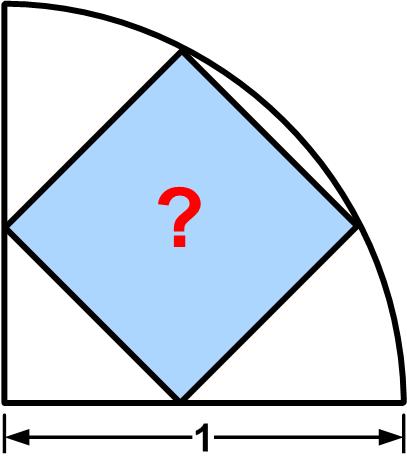 Another
Another