 The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto. The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university.
The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto. The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university.
“If sn denotes the sum of the first n natural numbers, find the sum of the infinite series
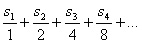 .”
.”
Unfortunately, the “Grade XIII” exam problem sets were not provided with answers, so I have no confirmation for my result. There may be a cunning way to manipulate the series to get a solution, but I could not see it off-hand. So I employed my tried and true power series approach to get my answer. It turned out to be power series manipulations on steroids, so there must be a simpler solution that does not use calculus. I assume the exams were timed exams, so I am not sure how a harried student could come up with a quick solution. I would appreciate any insights into this.
Answer.
See Serious Series for a solution.
(Update 1/18/2021, 9/6/2024) Other Solutions
Continue reading →
 Here is a challenging problem from the Polish Mathematical Olympiads published in 1960.
Here is a challenging problem from the Polish Mathematical Olympiads published in 1960.
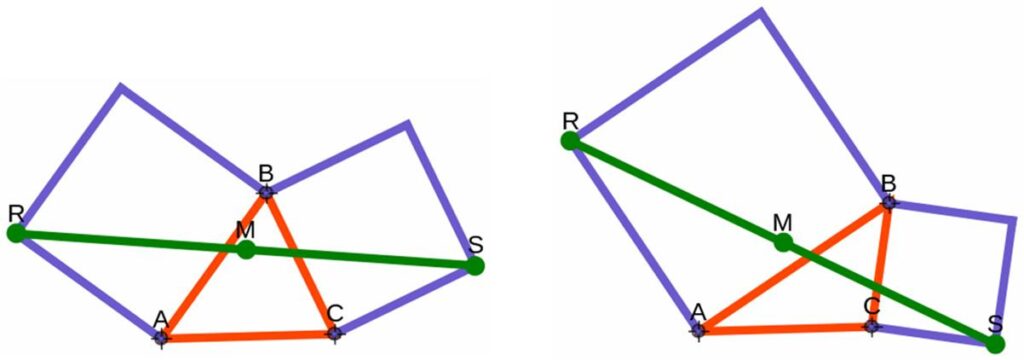
 Here is surprising problem from the 1875 The Analyst
Here is surprising problem from the 1875 The Analyst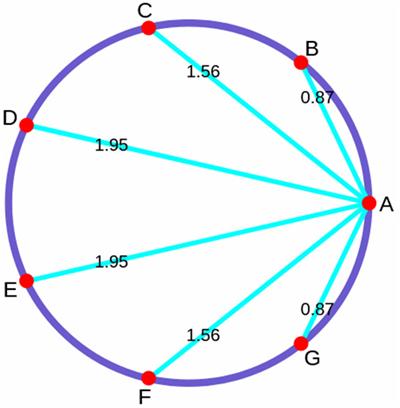 Futility Closet
Futility Closet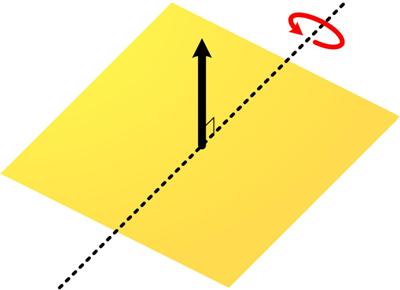 Here is another challenging problem from the first issue of the 1874 The Analyst, which also appears in Benjamin Wardhaugh’s book.
Here is another challenging problem from the first issue of the 1874 The Analyst, which also appears in Benjamin Wardhaugh’s book. Here is a fairly straight-forward problem from 500 Mathematical Challenges.
Here is a fairly straight-forward problem from 500 Mathematical Challenges. Here is another problem from the 2020 Math Calendar.
Here is another problem from the 2020 Math Calendar.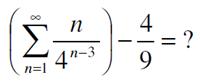
 The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto. The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university.
The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto. The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university. This is another problem from the 2020 Math Calendar.
This is another problem from the 2020 Math Calendar. Here is another problem from the 2020 Math Calendar to stimulate your mind.
Here is another problem from the 2020 Math Calendar to stimulate your mind.