 This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.
This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.
“Problem
For any positive integer, k, let Sk = {x1, x2, … , xn} be the set of [non-negative] real numbers for which x1 + x2 + … + xn = k and P = x1 x2 … xn is maximised. For example, when k = 10, the set {2, 3, 5} would give P = 30 and the set {2.2, 2.4, 2.5, 2.9} would give P = 38.25. In fact, S10 = {2.5, 2.5, 2.5, 2.5}, for which P = 39.0625.
Prove that P is maximised when all the elements of S are equal in value and rational.”
I took a different approach from Maths Challenge, but for me, it did not rely on remembering a somewhat obscure formula. (I don’t remember formulas well at my age—only procedures, processes, or proofs, which is ironic, since at a younger age it was just the opposite.) It is also clear from the Maths Challenge solution that the numbers were assumed to be non-negative.
See Maximum Product.
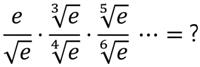 This is a delightful and surprising problem from Presh Talwalkar.
This is a delightful and surprising problem from Presh Talwalkar.
 If you will pardon the pun, this is a diabolical problem from the collection Five Hundred Mathematical Challenges.
If you will pardon the pun, this is a diabolical problem from the collection Five Hundred Mathematical Challenges. This 2005 four-star problem from Colin Hughes at Maths Challenge is also a bit challenging.
This 2005 four-star problem from Colin Hughes at Maths Challenge is also a bit challenging. This is another stimulating math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This is another stimulating math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net). This is a stimulating problem from the UKMT Senior Math Challenge for 2017. The additional problem “for investigation” is particularly challenging. (I have edited the problem slightly for clarity.)
This is a stimulating problem from the UKMT Senior Math Challenge for 2017. The additional problem “for investigation” is particularly challenging. (I have edited the problem slightly for clarity.) There is the famous chicken and the egg problem: If a chicken and a half can lay an egg and a half in a day and a half, how many eggs can three chickens lay in three days? Fibonacci 800 years ago in his book Liber Abaci (1202 AD) did not have exactly this problem (as far as I could find), but he posed its equivalent. And most likely the problem came even earlier from the Arabs. So we can essentially claim Fibonacci (or the Arabs) as the father of the chicken and egg problem. Here are three of Fibonacci’s actual problems:
There is the famous chicken and the egg problem: If a chicken and a half can lay an egg and a half in a day and a half, how many eggs can three chickens lay in three days? Fibonacci 800 years ago in his book Liber Abaci (1202 AD) did not have exactly this problem (as far as I could find), but he posed its equivalent. And most likely the problem came even earlier from the Arabs. So we can essentially claim Fibonacci (or the Arabs) as the father of the chicken and egg problem. Here are three of Fibonacci’s actual problems: This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.
This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.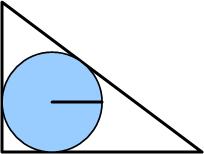 This statement showed up recently at
This statement showed up recently at  This is a delightful little problem from Dick Hess that exercises one’s basic facility with logarithms:
This is a delightful little problem from Dick Hess that exercises one’s basic facility with logarithms: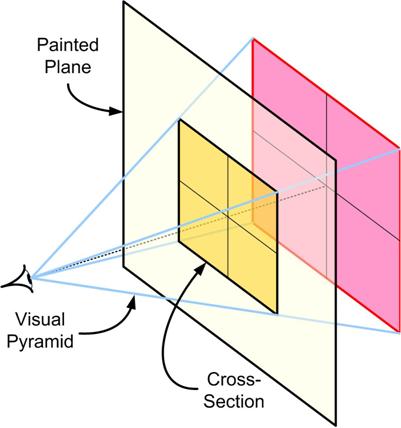 I was reading yet another book on the Scientific Revolution when I came across a discussion of the mathematical significance of the invention of perspective for painting in the 15th century Italian Renaissance. The main player in the saga was Leon Battista Alberti (1404 – 1472) and his tome De Pictura (On Painting) (1435-6), which contained the first mathematical presentation of perspective. Even though mathematics was advertised, it was not at the level of trigonometry I used in my post “
I was reading yet another book on the Scientific Revolution when I came across a discussion of the mathematical significance of the invention of perspective for painting in the 15th century Italian Renaissance. The main player in the saga was Leon Battista Alberti (1404 – 1472) and his tome De Pictura (On Painting) (1435-6), which contained the first mathematical presentation of perspective. Even though mathematics was advertised, it was not at the level of trigonometry I used in my post “