 Here is another problem from the 2020 Math Calendar to stimulate your mind.
Here is another problem from the 2020 Math Calendar to stimulate your mind.![]()
Remember that the answers to Math Calendar problems must all be whole numbers representing days of the month.
See New Years Sum for a solution.

 Here is another problem from the 2020 Math Calendar to stimulate your mind.
Here is another problem from the 2020 Math Calendar to stimulate your mind.![]()
Remember that the answers to Math Calendar problems must all be whole numbers representing days of the month.
See New Years Sum for a solution.
 This is a delightful and surprising problem from Presh Talwalkar.
This is a delightful and surprising problem from Presh Talwalkar.
“This puzzle was created by a MindYourDecisions fan in India. What is the value of the infinite product? The numerators are the odd nth roots of [Euler’s constant] e and the denominators are even nth roots of e.”
See Euler Magic for a solution.
 If you will pardon the pun, this is a diabolical problem from the collection Five Hundred Mathematical Challenges.
If you will pardon the pun, this is a diabolical problem from the collection Five Hundred Mathematical Challenges.
“Problem 5. Calculate the sum![]()
__________
It has a non-calculus solution, but that involves a bunch of manipulations that were not that evident to me, or at least I doubt if I could have come up with them. I was able to reframe the problem using one of my favorite approaches, power series (or polynomials). The calculations are a bit hairy in any case, but I was impressed that my method worked at all.
See the Number of the Beast for solutions.
 This 2005 four-star problem from Colin Hughes at Maths Challenge is also a bit challenging.
This 2005 four-star problem from Colin Hughes at Maths Challenge is also a bit challenging.
“Problem
For any set of real numbers, R = {x, y, z}, let sum of pairwise products,
________________S = xy + xz + yz.
Given that x + y + z = 1, prove that S ≤ 1/3.”
Again, I took a different approach from Maths Challenge, whose solution began with an unexplained premise.
See the Pairwise Products
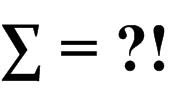 This is another stimulating math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This is another stimulating math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net).
“Problem
Find the exact value of the following infinite series:
1/2! + 2/3! + 3/4! + 4/5! + …”
See the Unexpected Sum for solutions.
 This is a stimulating problem from the UKMT Senior Math Challenge for 2017. The additional problem “for investigation” is particularly challenging. (I have edited the problem slightly for clarity.)
This is a stimulating problem from the UKMT Senior Math Challenge for 2017. The additional problem “for investigation” is particularly challenging. (I have edited the problem slightly for clarity.)
“The parabola with equation y = x² is reflected about the line with equation y = x + 2. Which of the following is the equation of the reflected parabola?
A_x = y² + 4y + 2_____B_x = y² + 4y – 2_____C_x = y² – 4y + 2
D_x = y² – 4y – 2_____E_x = y² + 2
For investigation: Find the coordinates of the point that is obtained when the point with coordinates (x, y) is reflected about the line with equation y = mx + b.”
See Flipping Parabolas for a solution.
 There is the famous chicken and the egg problem: If a chicken and a half can lay an egg and a half in a day and a half, how many eggs can three chickens lay in three days? Fibonacci 800 years ago in his book Liber Abaci (1202 AD) did not have exactly this problem (as far as I could find), but he posed its equivalent. And most likely the problem came even earlier from the Arabs. So we can essentially claim Fibonacci (or the Arabs) as the father of the chicken and egg problem. Here are three of Fibonacci’s actual problems:
There is the famous chicken and the egg problem: If a chicken and a half can lay an egg and a half in a day and a half, how many eggs can three chickens lay in three days? Fibonacci 800 years ago in his book Liber Abaci (1202 AD) did not have exactly this problem (as far as I could find), but he posed its equivalent. And most likely the problem came even earlier from the Arabs. So we can essentially claim Fibonacci (or the Arabs) as the father of the chicken and egg problem. Here are three of Fibonacci’s actual problems:
By modern standards these problems all involve simple arithmetic to solve. But there are actually some subtleties in mapping the mathematical model to the situation, in which fractions, proportions, ratios, and “direct variation” get swirled into the mix—naturally causing some confusion.
See Fibonacci, Chickens, and Proportions for a solution.
 This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.
This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.
“Problem
For any positive integer, k, let Sk = {x1, x2, … , xn} be the set of [non-negative] real numbers for which x1 + x2 + … + xn = k and P = x1 x2 … xn is maximised. For example, when k = 10, the set {2, 3, 5} would give P = 30 and the set {2.2, 2.4, 2.5, 2.9} would give P = 38.25. In fact, S10 = {2.5, 2.5, 2.5, 2.5}, for which P = 39.0625.
Prove that P is maximised when all the elements of S are equal in value and rational.”
I took a different approach from Maths Challenge, but for me, it did not rely on remembering a somewhat obscure formula. (I don’t remember formulas well at my age—only procedures, processes, or proofs, which is ironic, since at a younger age it was just the opposite.) It is also clear from the Maths Challenge solution that the numbers were assumed to be non-negative.
See Maximum Product.
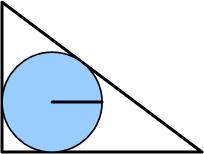 This statement showed up recently at Futility Closet and I found it to be another one of those magical results that seemed so surprising. I don’t recall ever seeing this before.
This statement showed up recently at Futility Closet and I found it to be another one of those magical results that seemed so surprising. I don’t recall ever seeing this before.
“The radius of a circle inscribed in a 3-4-5 triangle is 1.
(In fact, the inradius of any Pythagorean triangle is an integer.)”
(A Pythagorean triangle is a right triangle whose sides form a Pythagorean triple.) Futility Closet left these remarkable statements unproven, so naturally I felt I had to provide a proof.
 This is a delightful little problem from Dick Hess that exercises one’s basic facility with logarithms:
This is a delightful little problem from Dick Hess that exercises one’s basic facility with logarithms:
“Define x as ![]()
Find an expression for ![]()
in terms of x where the only constants appearing are integers.”
See the Logging Problem for a solution.