
This is from the UKMT Senior Challenge of 1999.
What is the sum to infinity of the convergent series![]()
A_7/4_____B_2_____C_√5_____D_9/4_____E_7/3”
See Fibonacci Fandango for a solution.


This is from the UKMT Senior Challenge of 1999.
What is the sum to infinity of the convergent series![]()
A_7/4_____B_2_____C_√5_____D_9/4_____E_7/3”
See Fibonacci Fandango for a solution.
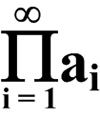 This is a challenging problem from Mathematical Quickies (1967).
This is a challenging problem from Mathematical Quickies (1967).
“Evaluate the infinite product:![]() ”
”
I came up with a motivated solution using some standard techniques from calculus. Mathematical Quickies had a solution that did not employ calculus, but one which I felt used unmotivated tricks.
See the Infinite Product Problem for solutions.
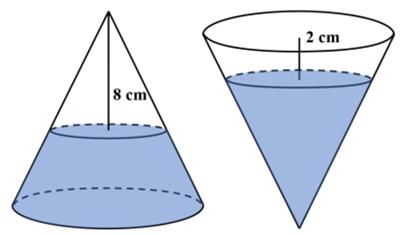 I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.
I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.
Presh Talwalkar: “This was sent to me as a competition problem for 8th graders, so it would be a challenge problem for students aged 12 to 13. When a conical bottle rests on its flat base, the water in the bottle is 8 cm from its vertex. When the same conical bottle is turned upside down, the water level is 2 cm from its base. What is the height of the bottle? (Note “conical” refers to a right circular cone as is common usage.) I at first thought this problem was impossible. But it actually can be solved.”
See the Conical Bottle Problem for solutions.
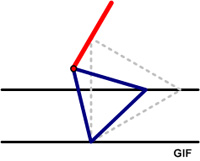 The following interesting behavior was found at the Futility Closet website:
The following interesting behavior was found at the Futility Closet website:
“A pleasing fact from David Wells’ Archimedes Mathematics Education Newsletter: Draw two parallel lines. Fix a point A on one line and move a second point B along the other line. If an equilateral triangle is constructed with these two points as two of its vertices, then as the second point moves, the third vertex C of the triangle will trace out a straight line. Thanks to reader Matthew Scroggs for the tip and the GIF.”
This is rather amazing and cries out for a proof. It also raises the question of how anyone noticed this behavior in the first place. I proved the result with calculus, but I wonder if there is a slicker way that makes it more obvious. See the Straight and Narrow Problem.
(Update 3/25/2019) Continue reading
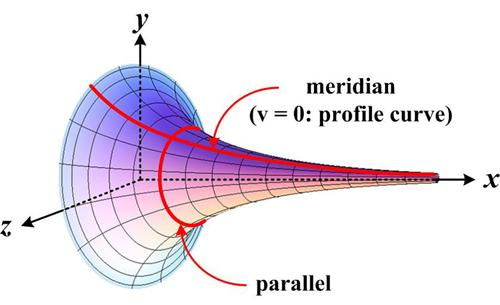 This essay began as an effort to prove Tanya Khovanova’s statement in her article “The Annoyance of Hyperbolic Surfaces” that her crocheted hyperbolic surface had constant (negative) curvature. I discussed Khovanova’s article in my previous essay “Exponential Yarn”. What I thought would be a fairly straight-forward exercise turned into a more concerted effort as I concluded that her crocheted surface did not have constant curvature. However, I found additional references that supported her statement, so I was becoming quite confused. I looked at other, similar surfaces to try to understand the whole curvature situation. This involved a lot of tedious computations (with my usual plethora of mistakes) that proved most challenging. But then I realized where I had gone astray. To cover my ignorance I claimed my error stemmed from a subtle misunderstanding. Herewith is a presentation of what I found. See Bugles, Trumpets, and Beltrami.
This essay began as an effort to prove Tanya Khovanova’s statement in her article “The Annoyance of Hyperbolic Surfaces” that her crocheted hyperbolic surface had constant (negative) curvature. I discussed Khovanova’s article in my previous essay “Exponential Yarn”. What I thought would be a fairly straight-forward exercise turned into a more concerted effort as I concluded that her crocheted surface did not have constant curvature. However, I found additional references that supported her statement, so I was becoming quite confused. I looked at other, similar surfaces to try to understand the whole curvature situation. This involved a lot of tedious computations (with my usual plethora of mistakes) that proved most challenging. But then I realized where I had gone astray. To cover my ignorance I claimed my error stemmed from a subtle misunderstanding. Herewith is a presentation of what I found. See Bugles, Trumpets, and Beltrami.
(Update 4/6/2019) Continue reading
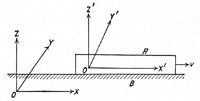 Over the years one of the subjects I return to periodically to study is Einstein’s Theory of Relativity, both the Special and General theories. Interest in the Special Theory focused on the derivation of the Lorentz transformations (or contractions). Why did objects appear with different lengths and clocks run at different speeds for observers moving relative to one another? Early on (late 60s) I came across a great explanation in the 1923 book by C. P. Steinmetz. He derived it from two general assumptions of special relativity: (1) that all motion is relative, the motion of the railway train relative to the track being the same as the motion of the track relative to the train, and (2) that the laws of nature, and thus the velocity of light, are the same everywhere. I did not follow his derivation completely, so I produced my own, which I will give here. See the Lorentz Transformation.
Over the years one of the subjects I return to periodically to study is Einstein’s Theory of Relativity, both the Special and General theories. Interest in the Special Theory focused on the derivation of the Lorentz transformations (or contractions). Why did objects appear with different lengths and clocks run at different speeds for observers moving relative to one another? Early on (late 60s) I came across a great explanation in the 1923 book by C. P. Steinmetz. He derived it from two general assumptions of special relativity: (1) that all motion is relative, the motion of the railway train relative to the track being the same as the motion of the track relative to the train, and (2) that the laws of nature, and thus the velocity of light, are the same everywhere. I did not follow his derivation completely, so I produced my own, which I will give here. See the Lorentz Transformation.
 I came across the following problem from an Italian high school exam on the British Aperiodical website presented by Adam Atkinson:
I came across the following problem from an Italian high school exam on the British Aperiodical website presented by Adam Atkinson:
“There have been various stories in the Italian press and discussion on a Physics teaching mailing list I’m accidentally on about a question in the maths exam for science high schools in Italy last week. The question asks students to confirm that a given formula is the shape of the surface needed for a comfortable ride on a bike with square wheels.![]()
What do people think? Would this be a surprising question at A-level in the UK or in the final year of high school in the US or elsewhere?”
I had seen videos of riding a square-wheeled bicycle over a corrugated surface before, but I had never inquired about the nature of the surface. So I thought it would be a good time to see if I could prove the surface (cross-section) shown would do the job. See Square Wheels.
(Update 9/14/2023) Square Bridge That Rolls!
 This is an incredible application of the rolling square wheels idea described on Matt Parker’s Stand-up Maths Youtube website. It also demonstrates the difference between engineering and pure math. The engineers had to solve some challenging problems to adapt the theoretical math to a practical application. And such solutions are always required under tight time constrictions. Engineering certainly is a noble profession.
This is an incredible application of the rolling square wheels idea described on Matt Parker’s Stand-up Maths Youtube website. It also demonstrates the difference between engineering and pure math. The engineers had to solve some challenging problems to adapt the theoretical math to a practical application. And such solutions are always required under tight time constrictions. Engineering certainly is a noble profession.
 When our daughter-in-law made wheat shocks as center-pieces for hers and our son’s fall-themed wedding reception, I naturally could not help pointing out the age-old observation that they represented a hyperboloid of one sheet. This was naturally greeted with the usual groans, but the thought stayed with me as I realized I had never proved this mathematically to myself. And so I did.
When our daughter-in-law made wheat shocks as center-pieces for hers and our son’s fall-themed wedding reception, I naturally could not help pointing out the age-old observation that they represented a hyperboloid of one sheet. This was naturally greeted with the usual groans, but the thought stayed with me as I realized I had never proved this mathematically to myself. And so I did.
See the Hyperboloid as Ruled Surface.
(Updates 10/9/2020, 9/19/2022) Spinning Rod Demo, Spinning Umbrella
Continue reading
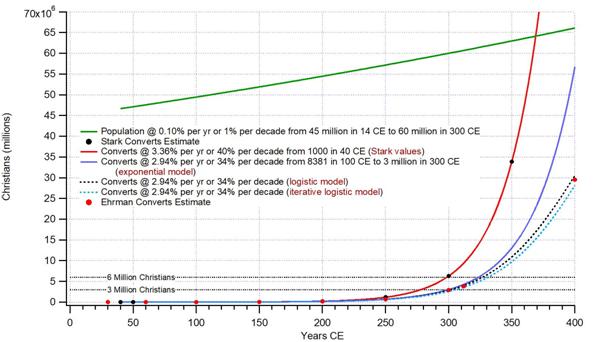 This was a catchy, misleading title that I could not resist, since my essay is not about math vs. religion as one might expect from the title, but rather about math helping religion. Back in 2016 I was reading Dr. Bart D. Ehrman’s blog that he was writing in preparation for his eventual book, The Triumph of Christianity, in which he was considering Rodney Stark’s purely mathematical analysis of the growth of Christianity in the first three centuries. Neither Rodney Stark nor Bart Ehrman described explicitly the underlying mathematical models of exponential growth that they were using and exactly what was meant by a rate of growth. Given the natural audience for the subject, these omissions were not surprising. So I thought I would clarify the math and also offer some variations on the models, which eventually reflected the actual situation more faithfully. See Math and Religion.
This was a catchy, misleading title that I could not resist, since my essay is not about math vs. religion as one might expect from the title, but rather about math helping religion. Back in 2016 I was reading Dr. Bart D. Ehrman’s blog that he was writing in preparation for his eventual book, The Triumph of Christianity, in which he was considering Rodney Stark’s purely mathematical analysis of the growth of Christianity in the first three centuries. Neither Rodney Stark nor Bart Ehrman described explicitly the underlying mathematical models of exponential growth that they were using and exactly what was meant by a rate of growth. Given the natural audience for the subject, these omissions were not surprising. So I thought I would clarify the math and also offer some variations on the models, which eventually reflected the actual situation more faithfully. See Math and Religion.
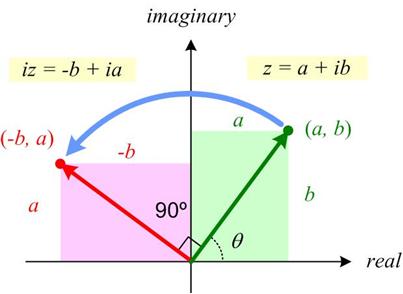 This may be a futile attempt at an elementary introduction to complex variables by emphasizing their geometric properties. The elementary part is probably undermined by an initial discussion of field extensions and a necessary reference to trigonometry. Hopefully, the suppression of the explicit use of complex powers of Euler’s constant e until the very end will allow the geometric ideas to have center stage. A primary goal of the essay is to realize that complex polynomials involve sums of circles in the plane. The image of real polynomials as wavy curves in the plane is misleading for an understanding of complex behavior. See Complex Numbers – Geometric Viewpoint.
This may be a futile attempt at an elementary introduction to complex variables by emphasizing their geometric properties. The elementary part is probably undermined by an initial discussion of field extensions and a necessary reference to trigonometry. Hopefully, the suppression of the explicit use of complex powers of Euler’s constant e until the very end will allow the geometric ideas to have center stage. A primary goal of the essay is to realize that complex polynomials involve sums of circles in the plane. The image of real polynomials as wavy curves in the plane is misleading for an understanding of complex behavior. See Complex Numbers – Geometric Viewpoint.