 I recently watched a remarkable and surprising interview on Numberphile of the actress Danica McKellar. She began as a child actress and recently has played romantic roles on the Hallmark series of TV movies. So it comes as a surprise to find she was an undergraduate math major, and with a female colleague and the help of their advisor one summer proved a theorem involving math and metallurgy.
I recently watched a remarkable and surprising interview on Numberphile of the actress Danica McKellar. She began as a child actress and recently has played romantic roles on the Hallmark series of TV movies. So it comes as a surprise to find she was an undergraduate math major, and with a female colleague and the help of their advisor one summer proved a theorem involving math and metallurgy.
She was terrifically articulate and enthusiastic during the interview and made a number of telling observations that would be helpful for any student, especially girls, who might find they like math in grade school and might even consider majoring in it in college.
Her big emphasis was on self-esteem and the importance of reaching girls to support any interest they might have in math against the negative forces they often experience. To this end she has written a series of math books, each tailored to a different grade-level of students. But she feels the middle school years are especially critical to support girls in math.
Perhaps the thing I liked best in the interview (maybe because it echoed my own views) was her attitude towards math—she loved solving puzzles. In fact, just doing math was its own reward. She politely deflected all efforts by Brady, the interviewer, to ask if she regretted not pursuing a professional career more devoted to math. Not to knock Brady’s fine interview but I found this line of questioning supporting the current utilitarian view of education (What good is it, how can it be of use to help me earn a living) to be a bit condescending. And there was even a whiff of what the most important thing to do with math and what the professors are training students for is math research. Since most math majors and even math Ph.D.s are not going to find employment in academia, math as an ancillary component to one’s career is the most one could imagine in this context. But above and beyond that is the real truth: math is fun for its own sake, and Danica McKellar championed that in spades. I don’t think I have seen anyone unabashedly extol the joys of doing math as well as she did.
I heartily recommend this interview to anyone, especially young girls, who might have a secret affection for mathematics but fear some stigma that might attach to them if they admitted it.
Some links from Youtube:
For a PDF version see Danica McKellar Interview.
 This is an interesting problem from the collection Five Hundred Mathematical Challenges.
This is an interesting problem from the collection Five Hundred Mathematical Challenges.
 In this moment when the collective actions of humans seem to be hurtling towards several cataclysms (burning up the planet, ending the American Experiment), I am reminded of a powerful image that invaded my psyche some 45 years ago. It was from Douglas Hofstadter’s magnum opus, Gödel, Escher, Bach (1979) and concerned his investigation of what became popularized as “emergent behavior” and “self-organization.” This was in the early days of chaos theory and Holland’s emerging complexity theory. Conway’s artificial life cellular automaton, the Game of Life, was the screen saver on countless computer terminals and burgeoning personal computers. It was also the time when neural nets were beginning to capture the imagination of machine learning researchers among the artificial intelligence community.
In this moment when the collective actions of humans seem to be hurtling towards several cataclysms (burning up the planet, ending the American Experiment), I am reminded of a powerful image that invaded my psyche some 45 years ago. It was from Douglas Hofstadter’s magnum opus, Gödel, Escher, Bach (1979) and concerned his investigation of what became popularized as “emergent behavior” and “self-organization.” This was in the early days of chaos theory and Holland’s emerging complexity theory. Conway’s artificial life cellular automaton, the Game of Life, was the screen saver on countless computer terminals and burgeoning personal computers. It was also the time when neural nets were beginning to capture the imagination of machine learning researchers among the artificial intelligence community.
 This is a challenging problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website.
This is a challenging problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website. This is an interesting problem from 180 BC China.
This is an interesting problem from 180 BC China.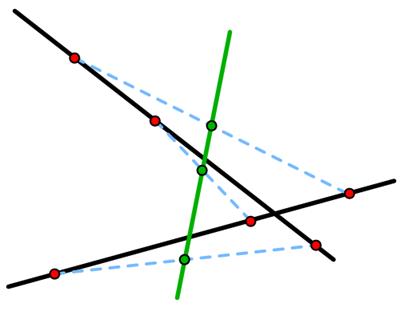 I came across this remarkable
I came across this remarkable 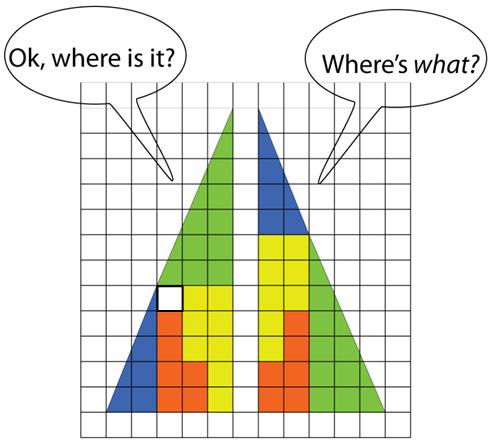 Coming across this
Coming across this  This is a clever puzzle from the 1986 AIME problems.
This is a clever puzzle from the 1986 AIME problems. This is an intriguing
This is an intriguing 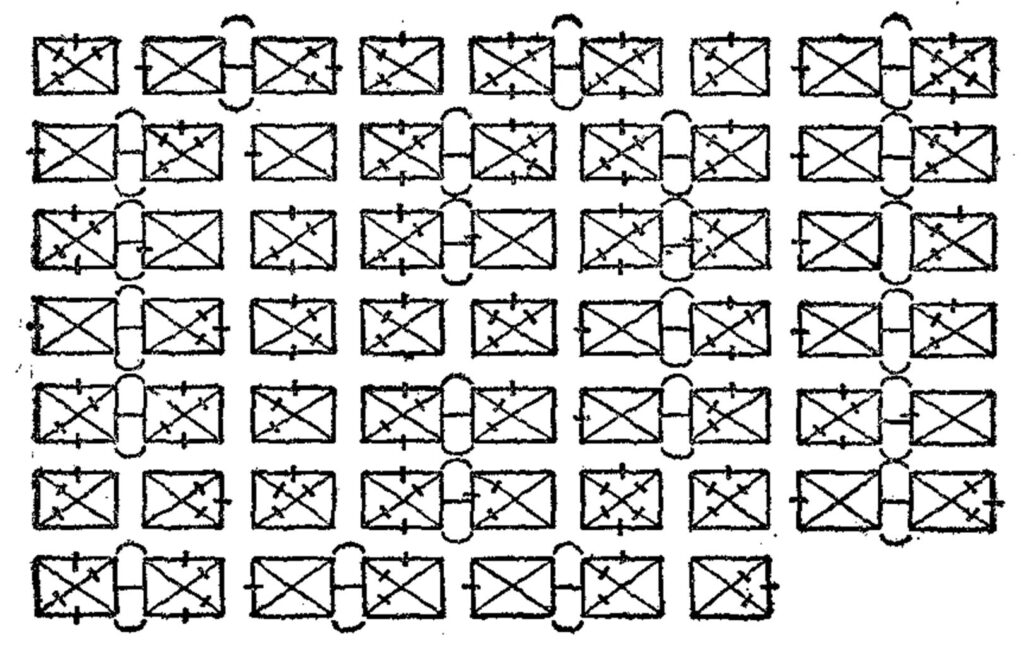
 In one of our periodic FaceTime calls I found out that my granddaughter in 6th grade was interested in learning algebra and had gotten a book to help her out. Clearly this initiative to get a head start prior to the normal course curriculum excited me, so I wrote what I thought was an insightful essay on the meaning and purpose of algebra. Needless to say it was an abysmal failure.
In one of our periodic FaceTime calls I found out that my granddaughter in 6th grade was interested in learning algebra and had gotten a book to help her out. Clearly this initiative to get a head start prior to the normal course curriculum excited me, so I wrote what I thought was an insightful essay on the meaning and purpose of algebra. Needless to say it was an abysmal failure.