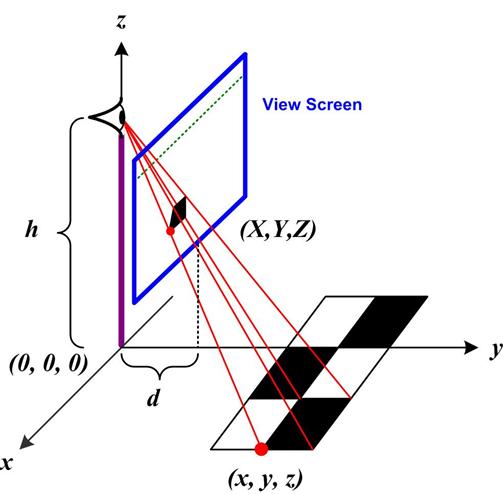
 A number of recent puzzles have involved perspective views of objects. I had never really explored the idea of a perspective map in detail. So some of the properties associated with it always seemed a bit vague to me. I decided I would derive the mathematical equations for the perspective or projective map and see how its properties fell out from the equations. With this information in hand I then addressed some questions I had about the article “Dürer: Disguise, Distance, Disagreements, and Diagonals!” by Annalisa Crannell, Marc Frantz, and Fumiko Futamura concerning a controversy over Albrecht Dürer’s woodcut St. Jerome in His Study (1514). And finally, I read somewhere that a parabola under a perspective map becomes an ellipse, so I was able to show that as well. See the Perspective Map.
A number of recent puzzles have involved perspective views of objects. I had never really explored the idea of a perspective map in detail. So some of the properties associated with it always seemed a bit vague to me. I decided I would derive the mathematical equations for the perspective or projective map and see how its properties fell out from the equations. With this information in hand I then addressed some questions I had about the article “Dürer: Disguise, Distance, Disagreements, and Diagonals!” by Annalisa Crannell, Marc Frantz, and Fumiko Futamura concerning a controversy over Albrecht Dürer’s woodcut St. Jerome in His Study (1514). And finally, I read somewhere that a parabola under a perspective map becomes an ellipse, so I was able to show that as well. See the Perspective Map.
(Update 7/1/2019)
For a more historical and less mathematical approach to the perspective map see my 1 July 2019 post on Alberti’s Perspective Construction.
