 Ian Stewart has a nice logic problem in his Casebook of Mathematical Mysteries, which includes a pastiche of Sherlock Holmes in the form of Herlock Soames and Dr. Watsup, along with brother Spycraft and nemesis Dr. Mogiarty.
Ian Stewart has a nice logic problem in his Casebook of Mathematical Mysteries, which includes a pastiche of Sherlock Holmes in the form of Herlock Soames and Dr. Watsup, along with brother Spycraft and nemesis Dr. Mogiarty.
“An important document was accidentally mislaid, and then stolen,” Spycraft said. “It is essential to the security of the British Empire that it be recovered without delay. If it gets into the hands of our enemies, careers will be ruined and parts of the Empire may fall. Fortunately, a local constable caught a glimpse of the thief, enough to narrow it down to precisely one of four men.”
“Petty thieves?”
“No, all four are gentlemen of high repute. Admiral Arbuthnot, Bishop Burlington, Captain Charlesworth, and Doctor Dashingham.”
Soames sat bolt upright. “Mogiarty has a hand in this, then.”
Not following his reasoning, I asked him to explain.
“All four are spies, Watsup. Working for Mogiarty.”
“Then … Spycraft must be engaged in counter-espionage!” I cried.
“Yes.” He glanced at his brother. “But you did not hear that from me.”
“Have these traitors been questioned?” I asked.
Spycraft handed me a dossier, and I read it aloud for Soames’s benefit. “Under interrogation Arbuthnot said ‘Burlington did it.’ Burlington said ‘Arbuthnot is lying.’ Charlesworth said ‘It was not I.’ Dashingham said ‘Arbuthnot did it.’ That is all.”
“Not quite all. We know from another source that exactly one of them was telling the truth.”
“You have an informer in Mogiarty’s inner circle, Spycraft?”
“We had an informer, Hemlock. He was garrotted with his own necktie before he could tell us the actual name. Very sad—it was an Old Etonian tie, totally ruined. However, all is not lost. If we can deduce who was the thief, we can obtain a search warrant and recover the document. All four men are being watched; they will have no opportunity to pass the document to Mogiarty. But our hands are tied; we must stick to the letter of the law. Moreover, if we raid the wrong premises, Mogiarty’s lawyers will publicise the mistake and cause irreparable damage.”
Which man was the thief?
Answer.
See the Purloined Papers Puzzle for solutions.
Post Views: 465
 Here is a challenging problem from the Polish Mathematical Olympiads published in 1960.
Here is a challenging problem from the Polish Mathematical Olympiads published in 1960.
 Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine.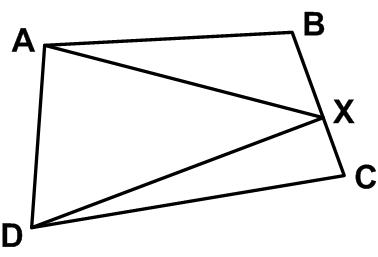 This is another simple problem from Five Hundred Mathematical Challenges:
This is another simple problem from Five Hundred Mathematical Challenges: This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008:
This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008: Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). Ian Stewart has a nice logic problem in his Casebook of Mathematical Mysteries, which includes a pastiche of Sherlock Holmes in the form of Herlock Soames and Dr. Watsup, along with brother Spycraft and nemesis Dr. Mogiarty.
Ian Stewart has a nice logic problem in his Casebook of Mathematical Mysteries, which includes a pastiche of Sherlock Holmes in the form of Herlock Soames and Dr. Watsup, along with brother Spycraft and nemesis Dr. Mogiarty.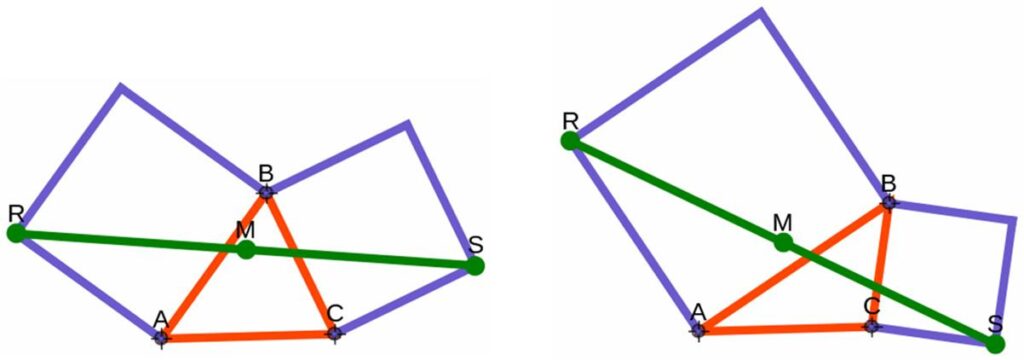
 Here is surprising problem from the 1875 The Analyst
Here is surprising problem from the 1875 The Analyst This is another simple problem from H. E. Dudeney.
This is another simple problem from H. E. Dudeney.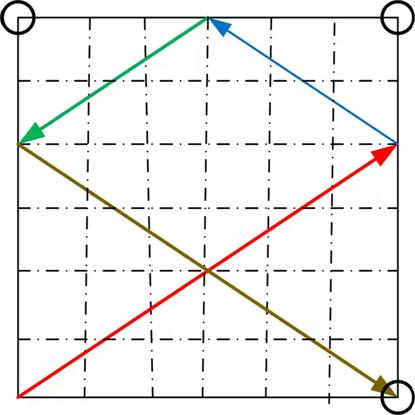 This is a nice
This is a nice