 This is a challenging problem from the 1986 American Invitational Mathematics Exam (AIME).
This is a challenging problem from the 1986 American Invitational Mathematics Exam (AIME).
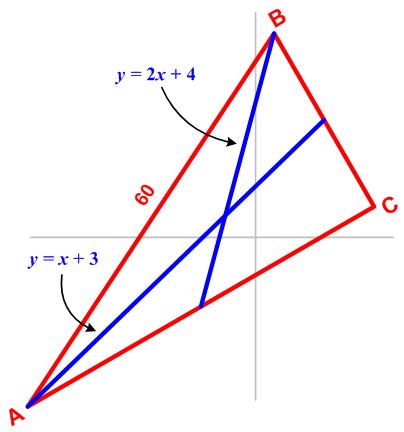
“Let triangle ABC be a right triangle in the xy-plane with a right angle at C. Given that the length of the hypotenuse AB is 60, and that the medians through A and B lie along the lines y = x + 3 and y = 2x + 4 respectively, find the area of triangle ABC.”
I have included a sketch to indicate that the sides of the right triangle are not parallel to the Cartesian coordinate axes.
The AIME (American Invitational Mathematics Examination) is an intermediate examination between the American Mathematics Competitions AMC 10 or AMC 12 and the USAMO (United States of America Mathematical Olympiad). All students who took the AMC 12 (high school 12th grade) and achieved a score of 100 or more out of a possible 150 or were in the top 5% are invited to take the AIME. All students who took the AMC 10 (high school 10th grade and below) and had a score of 120 or more out of a possible 150, or were in the top 2.5% also qualify for the AIME.
See the Challenging Triangle Problem for solutions.

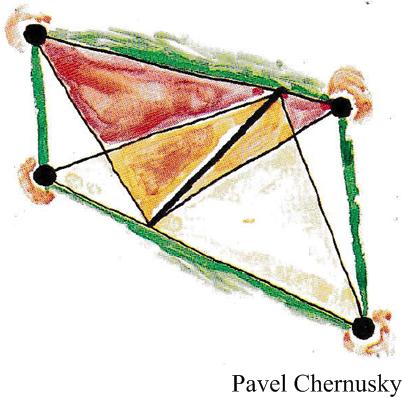 Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov.
Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov. Here is another logic problem from Ian Stewart.
Here is another logic problem from Ian Stewart.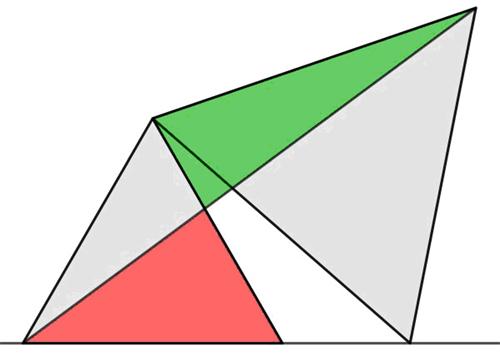 This is a most interesting problem proposed by
This is a most interesting problem proposed by 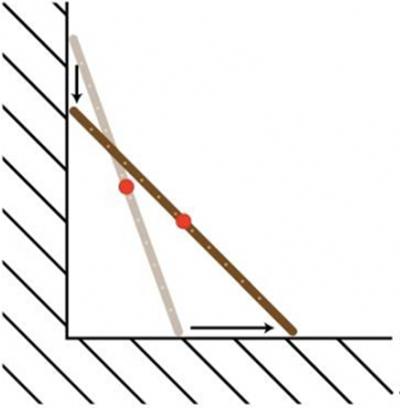 This is a thoughtful puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is a thoughtful puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.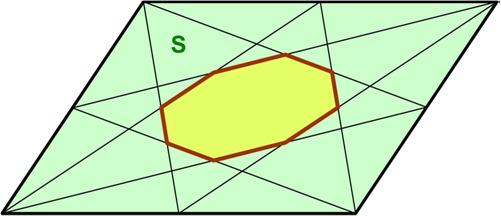 Here is another problem from the Polish Mathematical Olympiads published in 1960.
Here is another problem from the Polish Mathematical Olympiads published in 1960.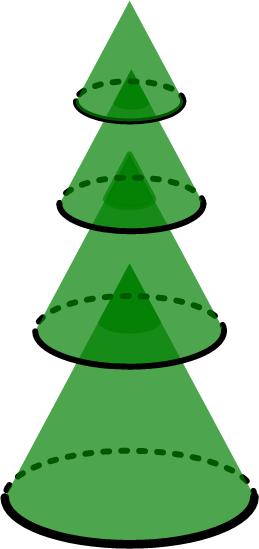 This is a belated Christmas puzzle from December 2019
This is a belated Christmas puzzle from December 2019  Here is another sum problem, this time from the 2021 Math Calendar.
Here is another sum problem, this time from the 2021 Math Calendar. This is another doable puzzle from Sam Loyd.
This is another doable puzzle from Sam Loyd.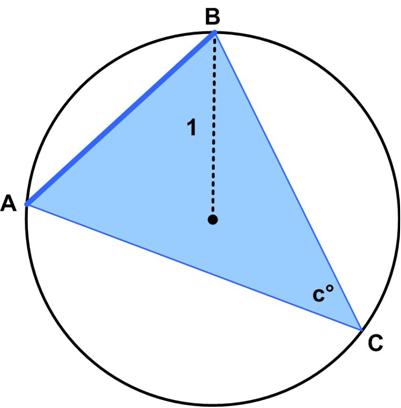 This is another nice puzzle from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.
This is another nice puzzle from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.