 This turns out to be an unambiguous, doable problem from the 19th century puzzle master Sam Loyd. It is based on an observation about jewelers’ signs of the times. I thought I would include Loyd’s narrative in its entirety.
This turns out to be an unambiguous, doable problem from the 19th century puzzle master Sam Loyd. It is based on an observation about jewelers’ signs of the times. I thought I would include Loyd’s narrative in its entirety.
“A CURIOUS paragraph has been going the rounds of the press which attempts to explain why the signs of the big watches in front of jewelry stores are always alike. They are painted upon the dial, apparently in a haphazard sort of a way, and yet they invariably indicate a certain number of minutes past eight. It cannot be attributable to chance, for it would tax one’s credulity to believe that such a coincidence could occur all over the civilized world.
There is no accepted rule or agreement established with the jewelers or sign painters, for careful inquiry proves that few of them are aware of the fact or ever noticed that any two are alike, it would be a marvelous case of unconscious imitation if it is looked upon as a mere custom, accidentally following a pattern set by the originator of the device of the sign of a big watch. In London, where they take pride in such things, I saw several big watches, looking as if they had hung in front of the stores for countless centuries, all indicating the same mysterious time, accompanied by the announcement that the firms were established a couple of hundred years ago. I do not doubt for a moment that some such similar sign can be found at Nuremberg, where the watch originated during the Fifteenth Century.
The discussion seems to have brought out a recognition of the fact that from an artistic point of view, symmetry requires that the hands should be evenly balanced, as it were, on both sides of the face of the watch.
If they are raised too much there is a certain “exasperating, declamatory effect,” which is not altogether pleasing.
The time would be incorrect if the hands pointed at 9 and 3, and at other points would be too low, so, as a matter of fact, and from an artistic point of view, the position is well selected and is one of the points which, with the aid of a watch, can be shown to be possible. It is a fact however, that the mere puzzle of telling what time the watch indicates, has been held up to public gaze for all these centuries without being thought of or solved?
Take your watch and set it to the time indicated, with the hands at equal distances from the six hour, which shows it to he a possible position, and then tell what time of the day it is! …”
Answer.
See A Question of Time for solutions.
Post Views: 580
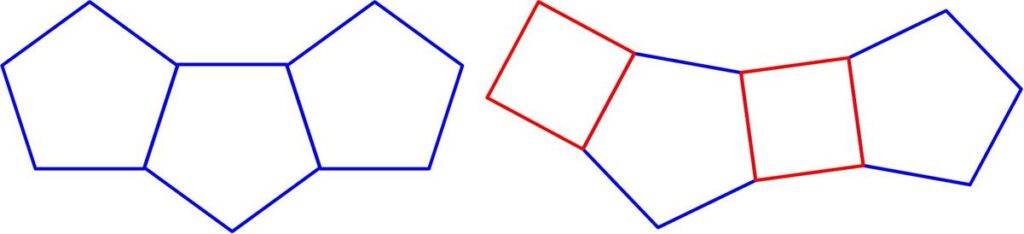 This is a nice geometric problem from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.
This is a nice geometric problem from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.
 In my post, “
In my post, “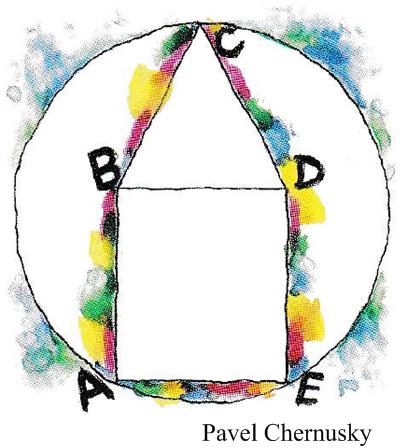 Here is another problem from the “Brainteasers” section of the Quantum magazine.
Here is another problem from the “Brainteasers” section of the Quantum magazine. I found these mazes on Twitter and thought they might make a relaxing puzzle interlude. They come from photographs of the street in front of the Museum of Mathematics (MoMath) in New York. The idea is to traverse the mazes from the Start to the Goal making only right turns. It was difficult working out the pattern of the green maze, especially the upper right corner.
I found these mazes on Twitter and thought they might make a relaxing puzzle interlude. They come from photographs of the street in front of the Museum of Mathematics (MoMath) in New York. The idea is to traverse the mazes from the Start to the Goal making only right turns. It was difficult working out the pattern of the green maze, especially the upper right corner.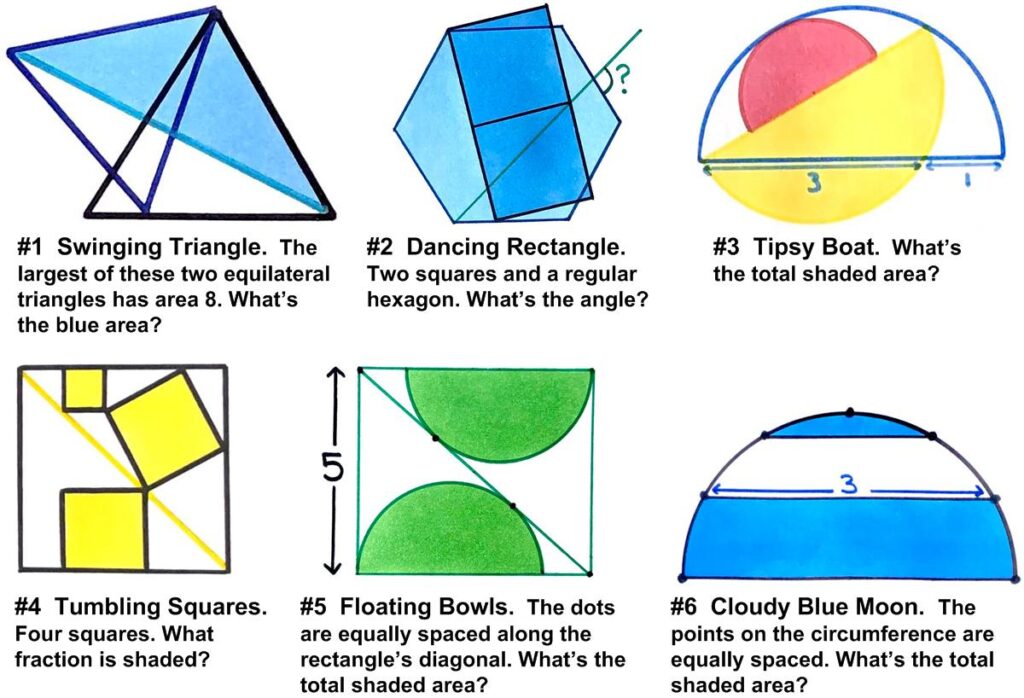 Here is yet another collection of beautiful, stimulating geometric problems from Catriona Agg (née Shearer).
Here is yet another collection of beautiful, stimulating geometric problems from Catriona Agg (née Shearer).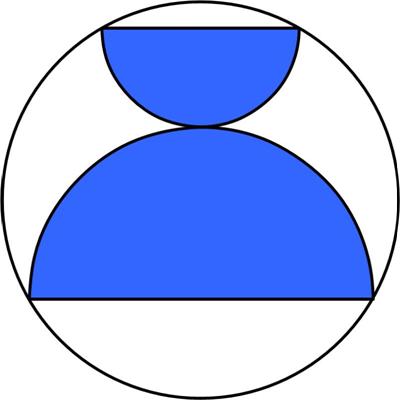 This is a nice brain tickling problem from
This is a nice brain tickling problem from  This turns out to be an unambiguous, doable problem from the 19th century puzzle master Sam Loyd. It is based on an observation about jewelers’ signs of the times. I thought I would include Loyd’s narrative in its entirety.
This turns out to be an unambiguous, doable problem from the 19th century puzzle master Sam Loyd. It is based on an observation about jewelers’ signs of the times. I thought I would include Loyd’s narrative in its entirety. Here is a seemingly simple problem from Futility Closet.
Here is a seemingly simple problem from Futility Closet. Here is a slightly different kind of problem from the Polish Mathematical Olympiads.
Here is a slightly different kind of problem from the Polish Mathematical Olympiads.