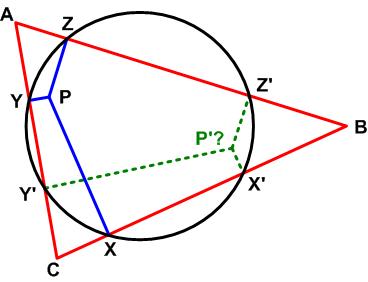
Twin Intersection Puzzle
 This is an interesting problem from the 1977 Canadian Math Society’s magazine, Crux Mathematicorum.
This is an interesting problem from the 1977 Canadian Math Society’s magazine, Crux Mathematicorum.
“206. [1977: 10] Proposed by Dan Pedoe, University of Minnesota.
A circle intersects the sides BC, CA and AB of a triangle ABC in the pairs of points X, X’, Y, Y’ and Z, Z’ respectively. If the perpendiculars at X, Y and Z to the respective sides BC, CA and AB are concurrent at a point P, prove that the respective perpendiculars at X’, Y’ and Z’ to the sides BC, CA and AB are concurrent at a point P’.”
See the Twin Intersection Puzzle
Puzzles and Problems: plane geometry, Dan Pedoe, Crux Mathematicorum
Pole Leveling Puzzle
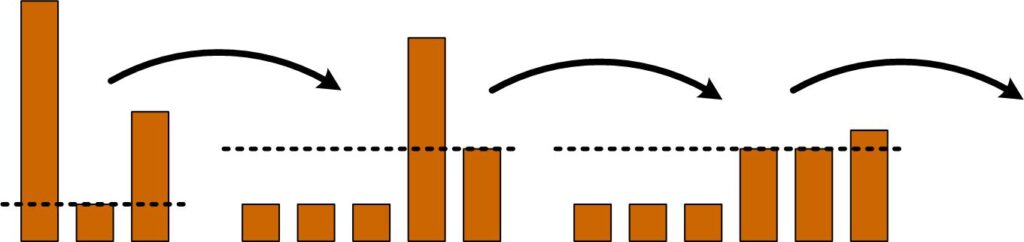
This is another thoughtful puzzle from the imaginative mind of James Tanton (with slight edits).
“Three poles of height 1183 feet, 182 feet, 637 feet stand in the ground. Pick a pole and saw off all the taller poles at that height. Plant those tops in the ground too. Repeat until no more such saw cuts can be made. Despite choices made along the way, what final result is sure to occur? [Four poles, heights a, b, c, d ft?]”
See the Pole Leveling Puzzle for a solution.
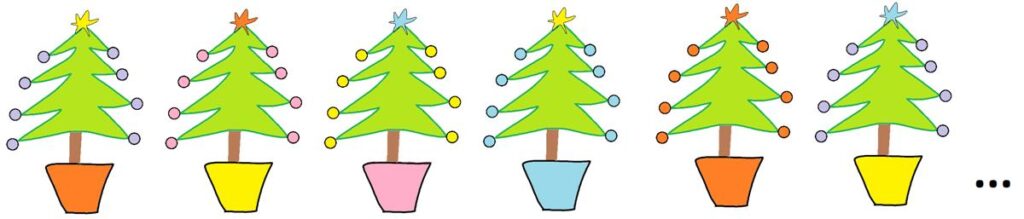
Christmas Tree Puzzle
James Tanton has come up with another imaginative concrete problem harboring a mathematical pattern.
“60 trees in a row. Their stars are yellow, orange, blue, Y, O, B, Y, O, B, … Their pots are orange, yellow, pink, blue, O, Y, P, B, O, Y, P, B, … Their baubles are mauve, pink, yellow, blue, orange, M, P, Y, B, O, M, P, Y, B, O, … Must there be an all yellow tree? All B? One with star = O, pot = O, baubles = M?”
See the Christmas Tree Puzzle for a solution.
Two Year Anniversary
 And so another year has passed—a pretty horrible one at that. Hopefully things mathematical have provided a distraction and entertainment.
And so another year has passed—a pretty horrible one at that. Hopefully things mathematical have provided a distraction and entertainment.
I thought I would update the retrospective from a year ago. Clearly, this eventful year made itself felt even through the statistics I gathered from the website. The growth the site experienced in posts read hit a plateau, but strangely, the number of new visitors increased a bit, at least for a while. That may have been due to the greater amount of free time away from the classroom that the virus demanded.
Shy Angle Problem
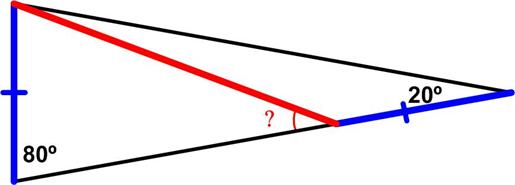 Here is yet another problem from Presh Talwalkar. This one is rather elegant in its simplicity of statement and answer.
Here is yet another problem from Presh Talwalkar. This one is rather elegant in its simplicity of statement and answer.
“Solve For The Angle – Viral Puzzle
I thank Barry and also Akshay Dhivare from India for suggesting this problem! This puzzle is popular on social media. What is the measure of the angle denoted by a “?” in the following diagram? You have to solve it using elementary geometry (no trigonometry or other methods). It’s harder than it looks. I admit I did not solve it. Can you figure it out?”
See the Shy Angle Problem for solutions.
Loggers Problem
 Here is another delightful problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Here is another delightful problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
“In Sussex, Holmes and I ran into a pair of woodcutters named Doug and Dave. There was an air of the unreliable about them—not helped by a clearly discernable aroma of scrumpy—but they nevertheless proved extremely helpful in guiding us to a particular hilltop clearing some distance outside of the town of Arundel. A shadowy group had been counterfeiting sorceries of a positively medieval kind, and all sorts of nastiness had ensued.
The Adventure of the Black Alchemist is not one that I would feel comfortable recounting, and if my life never drags me back to Chanctonbury Ring I shall be a happy man. But there is still some instructive material here. Whilst we were ascending our hill, Doug and Dave made conversation by telling us about their trade. According to these worthies, working together they were able to saw 600 cubic feet of wood into large logs over the course of a day, or split as much as 900 cubic feet of logs into chunks of firewood.
Holmes immediately suggested that they saw as much wood in the first part of the day as they would need in order to finish splitting it at the end of the day. It naturally fell to me to calculate precisely how much wood that would be.
Can you find the answer?”
See the Loggers Problem for solutions.
Barrier Minimal Path Problem
 This is a nifty little problem from the Quantum math magazine.
This is a nifty little problem from the Quantum math magazine.
“Two ants stand at opposite corners of a 1-meter square. A barrier was placed between them in the form of half a 1-meter square attached along the diagonal of the first square, as shown in the picture. One ant wants to walk to the other. How long is the shortest path?”
See the Barrier Minimal Path Problem for solutions.
Do I Avoid Kangaroos?
 This is a fun logic puzzle from one of Ian Stewart’s many math collections. I discovered that the problem actually is basically one of Lewis Carroll’s examples from an 1896 book:
This is a fun logic puzzle from one of Ian Stewart’s many math collections. I discovered that the problem actually is basically one of Lewis Carroll’s examples from an 1896 book:
- The only animals in this house are cats.
- Every animal that loves to gaze at the moon is suitable for a pet.
- When I detest an animal, I avoid it.
- No animals are meat-eaters, unless they prowl by night.
- No cat fails to kill mice.
- No Animals ever take to me, except those in this house.
- Kangaroos are not suitable for pets.
- Only meat-eaters kill mice.
- I detest animals that do not take to me.
- Animals that prowl at night love to gaze at the moon.
If all these statements are correct, do I avoid kangaroos, or not?
See Do I Avoid Kangaroos? for solutions.
Geometric Puzzle Marvels
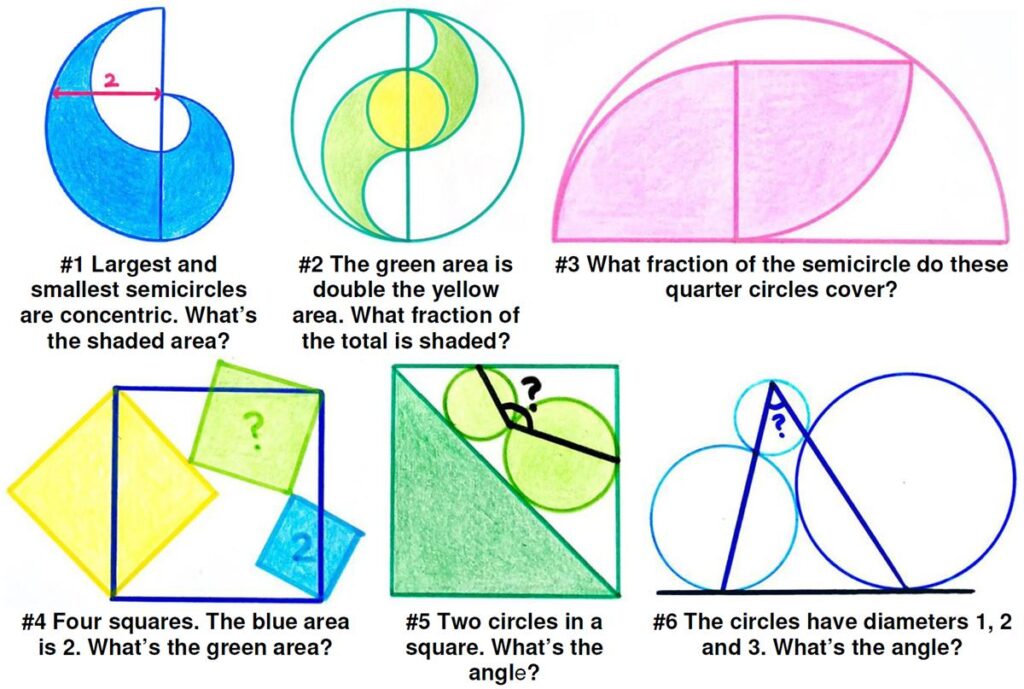
Here is another collection of beautiful geometric problems from Catriona Agg (née Shearer). They never fail to brighten the day with their loveliness.