 Manmohan Kaur took Arthur Conan Doyle’s popular 1903 Sherlock Holmes story “The Adventure of the Dancing Men” and used it in his math classes to illustrate the logic and mathematics involved in solving codes and ciphers. I thought his idea might work as a puzzle. It has been years since I read the story, so I had forgotten the decryption and found it quite doable from the setup provided by Kaur. Here is his presentation, subject to further edits and reductions in size on my part.
Manmohan Kaur took Arthur Conan Doyle’s popular 1903 Sherlock Holmes story “The Adventure of the Dancing Men” and used it in his math classes to illustrate the logic and mathematics involved in solving codes and ciphers. I thought his idea might work as a puzzle. It has been years since I read the story, so I had forgotten the decryption and found it quite doable from the setup provided by Kaur. Here is his presentation, subject to further edits and reductions in size on my part.
“The original story has been shortened and simplified. Reference to England has been completely removed and some other superfluous information that distracts the reader instead of helping solve the mystery have been omitted. In the original story Elriges is the name of an inn but we have taken the liberty to use it loosely as the name of a town.
The pictures of all stick figure messages except the fourth are from the collection The Return of Sherlock Holmes. The original story has a typographical error that throws off the decryption scheme. To remove this (intentional or unintentional) error, the fourth figure has been taken from Trap and Washington’s Introduction to Cryptography with Coding Theory. The fourth message is meant to have a different handwriting, so this serves our purposes well.
Condensed Story
Hilton Cubitt of Elriges visits you and gives you a paper with the following mysterious sequence of stick figures that he found lying on the sun-dial in his mansion.
Message 1:
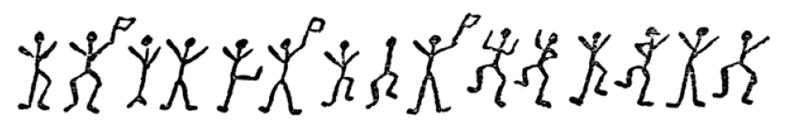
Cubitt explains that he recently married a Chicago woman named Elsie Patrick. Before the wedding, she had asked him never to ask about her past, as she had had some “very disagreeable associations” in her life, although she said that there was nothing that she was personally ashamed of. Their marriage had been a happy one until the messages began to arrive, first mailed from Chicago and then appearing in the garden of his mansion.
The messages had made Elsie very afraid but she did not explain the reasons for her fear, and Cubitt insisted on honoring his promise not to ask about Elsie’s life in Chicago. You look at the figures closely to understand them a little better and notice that some of the figures are holding flags. What could the flags mean? Perhaps the end of words?
The next morning Cubitt finds “a fresh crop of dancing men drawn in chalk upon the black wooden door of the tool-house”:
Message 2:

Two mornings later, “a fresh inscription had appeared”:
Message 3:
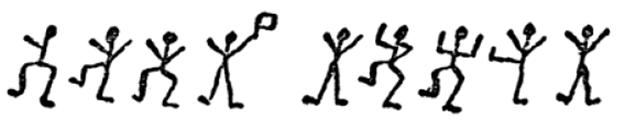
Three days later, “a message was left scrawled upon paper, and placed under a pebble upon the sun-dial”:
Message 4:
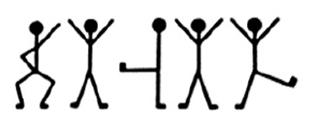
Cubitt gives copies of all these messages to you. Your task is to help him understand what is going on. You call your friend in the Chicago Police Department and ask her to find background information on Elsie Patrick. You learn that Elsie is the daughter of a Chicago crime boss, and was engaged to Abe Slaney, who worked for her dad, and that she had fled to escape her old life.
You examine all the occurrences of the dancing figures. Message 4 is in a different handwriting, so you guess that it is from a different person, most likely, Elsie, while messages 1, 2 and 3 are from the unknown person (the criminal). You spend the next two days trying to make some sense of the stick figures. You are now sure that the flags on some of the figures indicate the end of words. You also know that a simple substitution cipher is being used for the encryption, and that frequency analysis is the way to solve these ciphers.
Three days later, another message appears.
Message 5:
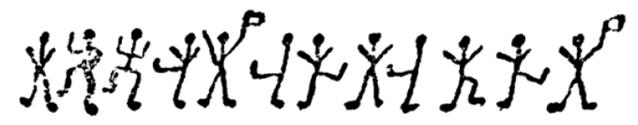
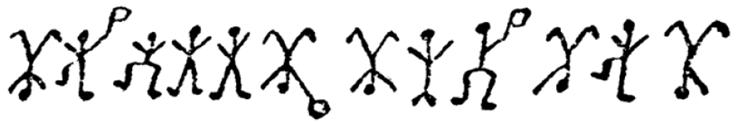 This message causes you to fear that the Cubitts are in immediate danger. You rush to Elriges and find Cubitt dead of a bullet to the heart and his wife gravely wounded from a gunshot to the head. What do the messages say?
This message causes you to fear that the Cubitts are in immediate danger. You rush to Elriges and find Cubitt dead of a bullet to the heart and his wife gravely wounded from a gunshot to the head. What do the messages say?
Inspector Martin of the Norfolk Constabulary believes that it is a murder-suicide attempt; Elsie is the prime suspect. But you, after noting some inconsistencies in that theory, know that there is a third person involved. How will you prove to Inspector Martin that a third person is involved?”
See The Mystery of the Dancing Men
 Here is another elegant Quantum math magazine Brainteaser problem.
Here is another elegant Quantum math magazine Brainteaser problem.
 This is an interesting problem from Posamentier and Lehmann’s Mathematical Curiosities.
This is an interesting problem from Posamentier and Lehmann’s Mathematical Curiosities. Manmohan Kaur took Arthur Conan Doyle’s popular 1903 Sherlock Holmes story “The Adventure of the Dancing Men” and used it in his math classes to illustrate the logic and mathematics involved in solving codes and ciphers. I thought his idea might work as a puzzle. It has been years since I read the story, so I had forgotten the decryption and found it quite doable from the setup provided by Kaur. Here is his
Manmohan Kaur took Arthur Conan Doyle’s popular 1903 Sherlock Holmes story “The Adventure of the Dancing Men” and used it in his math classes to illustrate the logic and mathematics involved in solving codes and ciphers. I thought his idea might work as a puzzle. It has been years since I read the story, so I had forgotten the decryption and found it quite doable from the setup provided by Kaur. Here is his 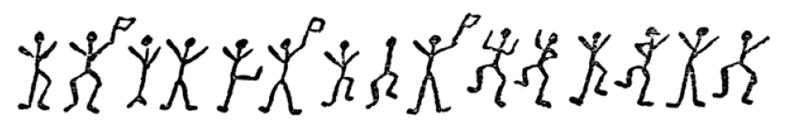

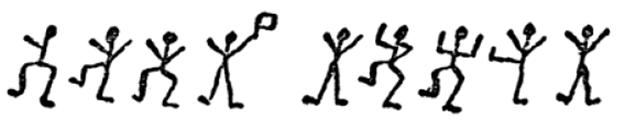
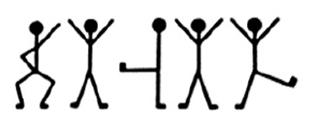
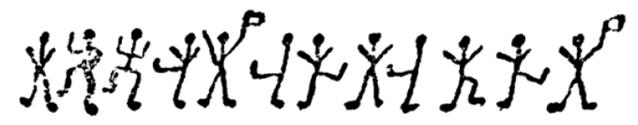
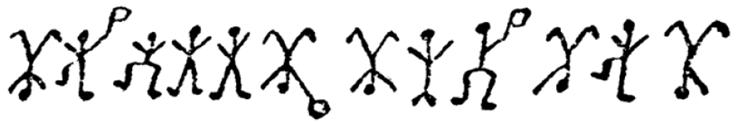 This message causes you to fear that the Cubitts are in immediate danger. You rush to Elriges and find Cubitt dead of a bullet to the heart and his wife gravely wounded from a gunshot to the head. What do the messages say?
This message causes you to fear that the Cubitts are in immediate danger. You rush to Elriges and find Cubitt dead of a bullet to the heart and his wife gravely wounded from a gunshot to the head. What do the messages say? This problem comes from the “Problems Drive” section of the Eureka magazine published in 1955 by the Archimedeans at Cambridge University, England. (“The problems drive is a competition conducted annually by the Archimedeans. Competitors work in pairs and are allowed five minutes per question ….”)
This problem comes from the “Problems Drive” section of the Eureka magazine published in 1955 by the Archimedeans at Cambridge University, England. (“The problems drive is a competition conducted annually by the Archimedeans. Competitors work in pairs and are allowed five minutes per question ….”)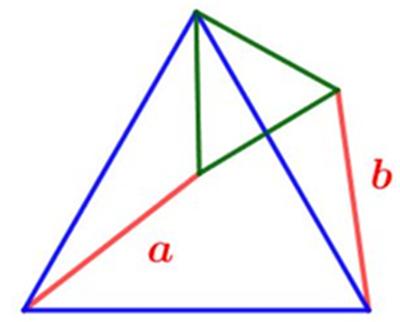 This is another problem from MEI’s MathsMonday.
This is another problem from MEI’s MathsMonday.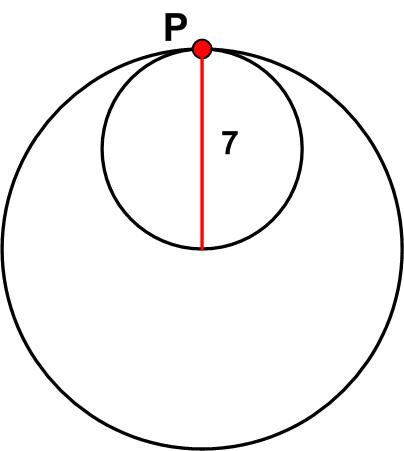 Here is an intriguing problem from the 2021 Math Calendar.
Here is an intriguing problem from the 2021 Math Calendar.
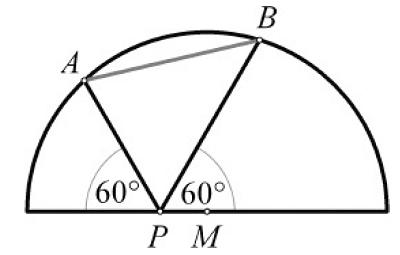
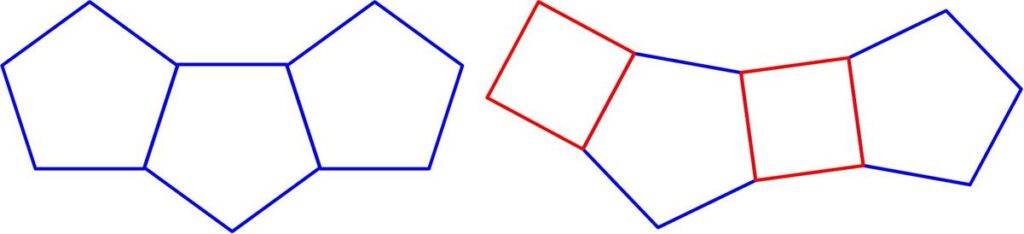 This is a nice geometric problem from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.
This is a nice geometric problem from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.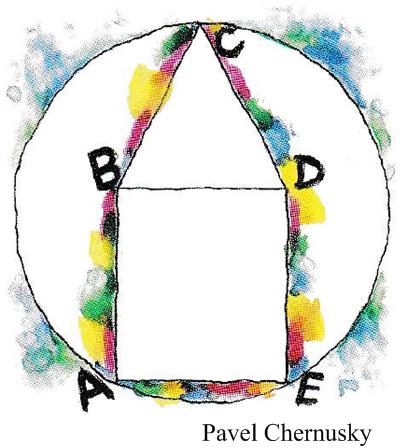 Here is another problem from the “Brainteasers” section of the Quantum magazine.
Here is another problem from the “Brainteasers” section of the Quantum magazine. I found these mazes on Twitter and thought they might make a relaxing puzzle interlude. They come from photographs of the street in front of the Museum of Mathematics (MoMath) in New York. The idea is to traverse the mazes from the Start to the Goal making only right turns. It was difficult working out the pattern of the green maze, especially the upper right corner.
I found these mazes on Twitter and thought they might make a relaxing puzzle interlude. They come from photographs of the street in front of the Museum of Mathematics (MoMath) in New York. The idea is to traverse the mazes from the Start to the Goal making only right turns. It was difficult working out the pattern of the green maze, especially the upper right corner.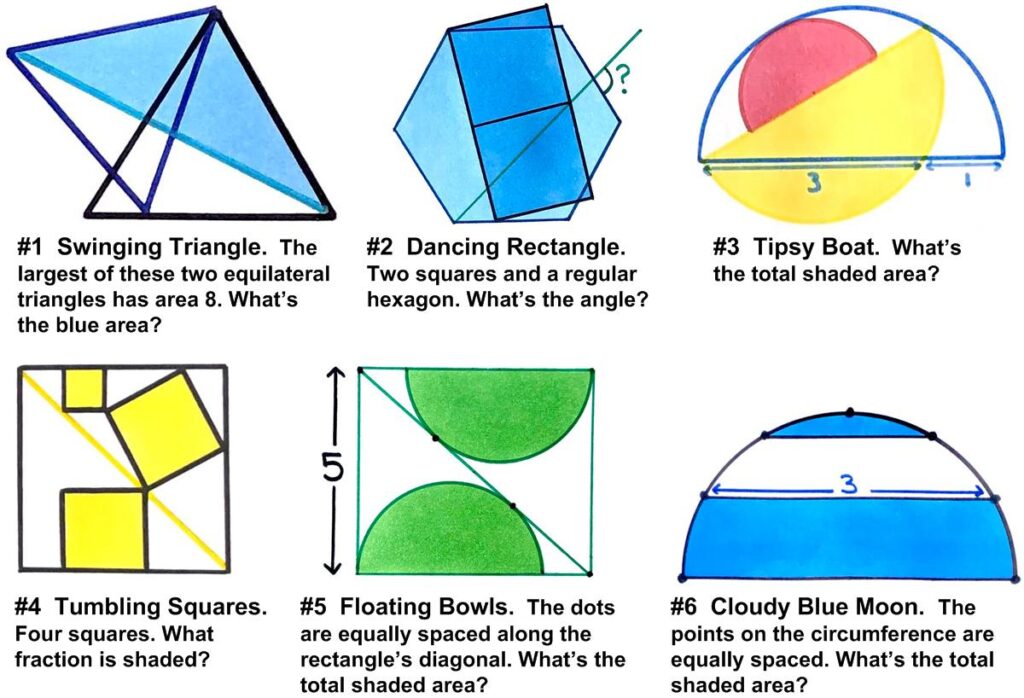 Here is yet another collection of beautiful, stimulating geometric problems from Catriona Agg (née Shearer).
Here is yet another collection of beautiful, stimulating geometric problems from Catriona Agg (née Shearer).