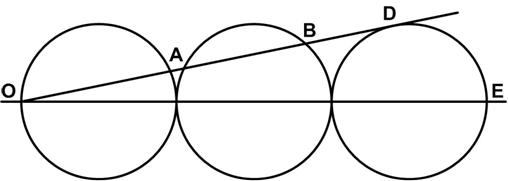
 This is a straight-forward problem by Geoffrey Mott-Smith from 1954.
This is a straight-forward problem by Geoffrey Mott-Smith from 1954.
“Three tangent circles of equal radius r are drawn, all centers being on the line OE. From O, the outer intersection of this axis with the left-hand circle, line OD is drawn tangent to the right-hand circle. What is the length, in terms of r, of AB, the segment of this tangent which forms a chord in the middle circle?”
See An Intercept Problem for solutions.

 This is another candle burning problem, presented by
This is another candle burning problem, presented by 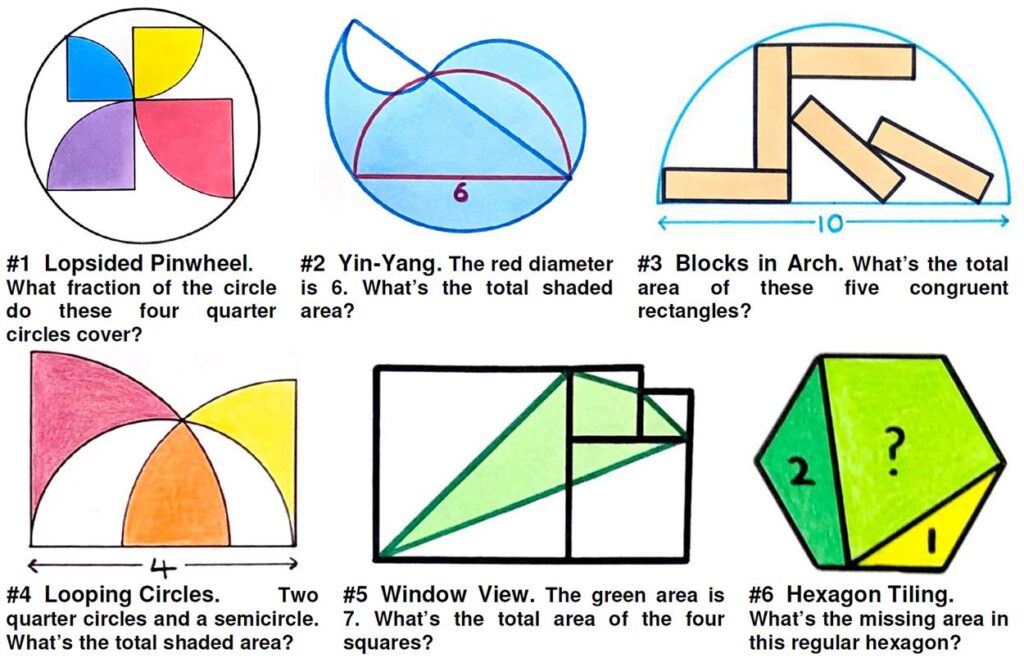 Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer).
Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer). This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2007:
This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2007: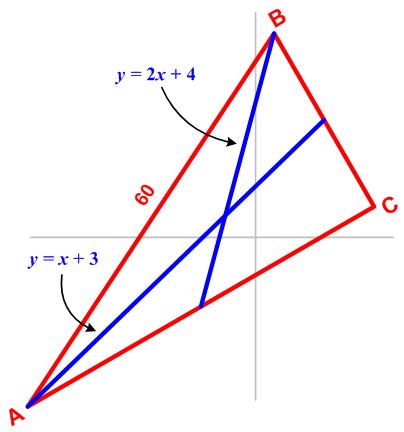 This is a challenging problem from the 1986 American Invitational Mathematics Exam (AIME).
This is a challenging problem from the 1986 American Invitational Mathematics Exam (AIME).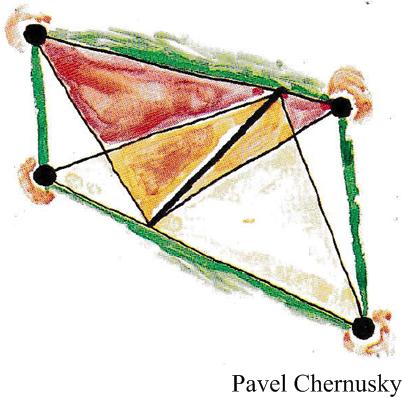 Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov.
Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov. Here is another logic problem from Ian Stewart.
Here is another logic problem from Ian Stewart.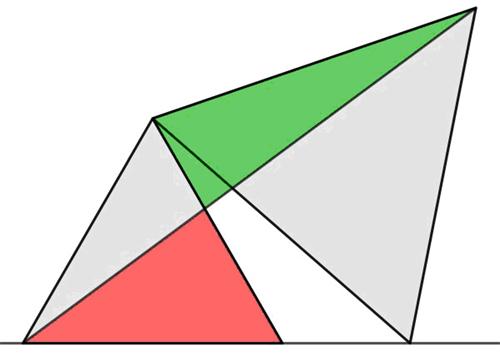 This is a most interesting problem proposed by
This is a most interesting problem proposed by 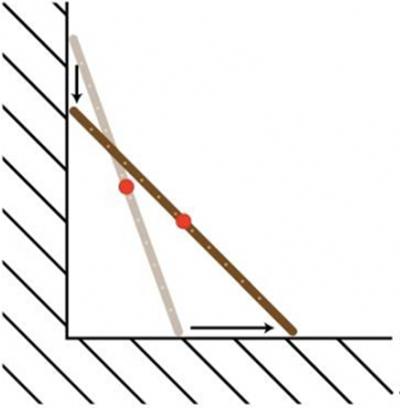 This is a thoughtful puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is a thoughtful puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.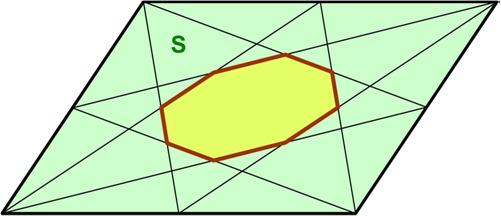 Here is another problem from the Polish Mathematical Olympiads published in 1960.
Here is another problem from the Polish Mathematical Olympiads published in 1960.