 For his Monday Puzzle in the Guardian Alex Bellos provided a seemingly impossible puzzle from the 1983 British teenager quiz show Blockbusters.
For his Monday Puzzle in the Guardian Alex Bellos provided a seemingly impossible puzzle from the 1983 British teenager quiz show Blockbusters.
“In the much-missed student quiz show Blockbusters, teenagers would ask host Bob Holness for a letter from a hexagonal grid. How we laughed when a contestant asked for a P! Holness would reply with a question in the following style: What P is an area of cutting edge mathematical research and also a process in the making of an espresso? The answer is the subject of today’s puzzle: percolation.
Today’s perplexing percolation poser concerns the following Blockbusters-style hexagonal grid:
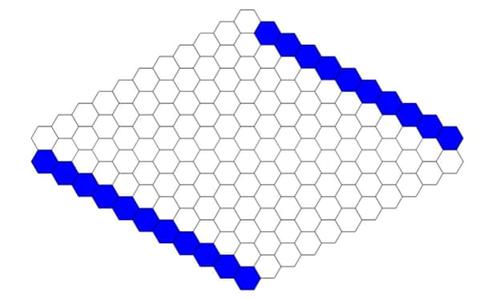
The grid above shows a 10×10 hexagonal tiling of a rhombus (i.e. a diamond shape), plus an outer row that demarcates the boundary of the rhombus. The boundary row on the top right and the bottom left are coloured blue, while the boundary row on the top left and the bottom right are white.
If we colour each hexagon in the rhombus either blue or white, one of two things can happen. Either there is a path of blue hexagons that connects the blue boundaries, such as here:
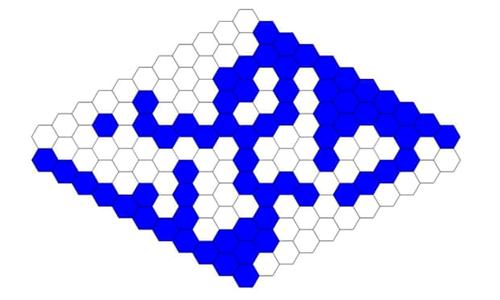
Or there is no path of blue hexagons that connects the blue boundaries, such as here:
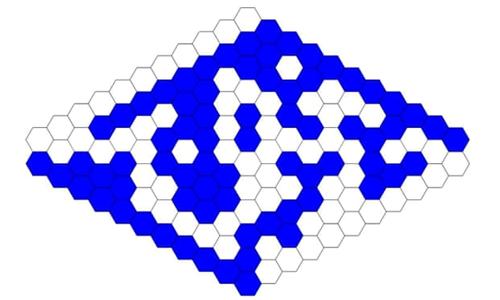
There are 100 hexagons in the rhombus. Since each of these hexagons can be either white or blue, the total number of possible configurations of white and blue hexagons in the rhombus is 2 x 2 x … x 2 one hundred times, or 2100, which is about 1,000,000,000,000,000,000,000,000,000,000.
In how many of these configurations is there a path of blue hexagons that connects the blue boundaries?
The answer requires a simple insight. Indeed, it is the insight on which the quiz show Blockbusters relied.
For clarification: a path of hexagons means a sequence of adjacent hexagons that are the same colour.”
Answer.
See the Blockbusters Problem for solution.
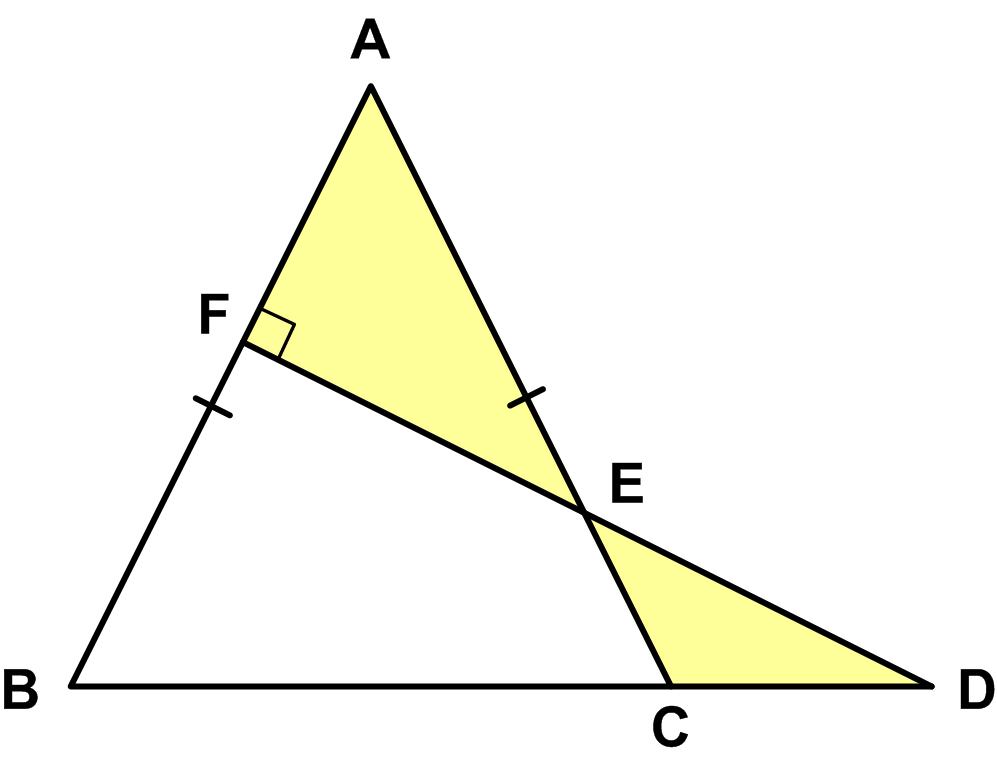 I found this problem from the 1981 Canadian Math Society’s magazine, Crux Mathematicorum, to be quite challenging.
I found this problem from the 1981 Canadian Math Society’s magazine, Crux Mathematicorum, to be quite challenging.
 Here is another Quantum math magazine Brainteaser.
Here is another Quantum math magazine Brainteaser. For his Monday Puzzle in the Guardian Alex Bellos provided a seemingly impossible
For his Monday Puzzle in the Guardian Alex Bellos provided a seemingly impossible 


 Here is another typical sum puzzle from Presh Talwalkar.
Here is another typical sum puzzle from Presh Talwalkar.

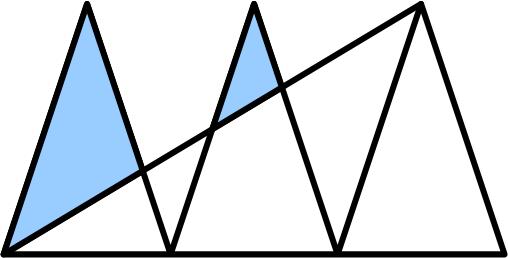 This is a nice little puzzle from the late Nick Berry’s Datagenetics Blog.
This is a nice little puzzle from the late Nick Berry’s Datagenetics Blog. This is an initially mind-boggling problem from the 1995 American Invitational Mathematics Exam (AIME).
This is an initially mind-boggling problem from the 1995 American Invitational Mathematics Exam (AIME). This puzzle from the Scottish Mathematical Council (SMC) Senior Mathematics Challenge seems at first to have insufficient information to solve.
This puzzle from the Scottish Mathematical Council (SMC) Senior Mathematics Challenge seems at first to have insufficient information to solve. Yet another year has passed, surprisingly, with perhaps the prospect of coming out from under the shadow of the pandemic. Again, I thought I would present the statistical pattern of interaction with the website in the absence of any explicit feedback.
Yet another year has passed, surprisingly, with perhaps the prospect of coming out from under the shadow of the pandemic. Again, I thought I would present the statistical pattern of interaction with the website in the absence of any explicit feedback.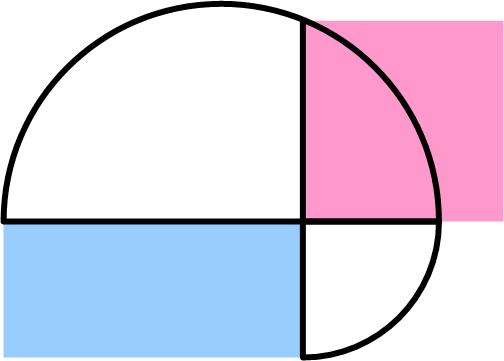 This is a provocative puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.
This is a provocative puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.