 This essay is slightly tangential to my usual fare, but it is prompted by a most amazing video that convinced me that the impact of AI this time is not hype, but rather a real threat to our society. I found the video at 3 Quarks Daily and it was of Johnny Cash singing a song called “Barbie Girl” to the tune of his trademark Folsom Prison Blues—only it wasn’t the late Johnny Cash (1932–2003), it was AI!
This essay is slightly tangential to my usual fare, but it is prompted by a most amazing video that convinced me that the impact of AI this time is not hype, but rather a real threat to our society. I found the video at 3 Quarks Daily and it was of Johnny Cash singing a song called “Barbie Girl” to the tune of his trademark Folsom Prison Blues—only it wasn’t the late Johnny Cash (1932–2003), it was AI!
See Voice Stealing
(Update 11/2/2023) I was wondering why the seeming lack of interest in this post, and then I tried the link to the video and found it has been removed from the public. There must be a reason, probably copyright issues somewhere, so even though I got a copy when it was public, I don’t think I should post it. This is really too bad, since it is in incredible example of what may be our dystopian future. I just rooted around and found another link that seems to be working. I have updated the text above.
(Update 5/4/2024) It gets worse. The Atlantic article “My Journey Inside the Voice-Clone Factory” shows what happens when voice-cloning is combined with image-cloning and OpenAI language models. It is a dystopian nightmare beyond imagining.
(Update 12/28/2025) And worse. Two recent, short articles show plausible scenarios for the rapidly approaching future. The first, “Digital Doppelganger — You and ‘You’ ”, dramatizes how the delegation of your public persona to AI apps ends up replacing you.
And the second, “How AI Is Taking Us Back To The Dark Ages”, shows how our increasing reliance on AI is delegating our independent thinking, so hard-won in the Enlightenment, back to a central authority.
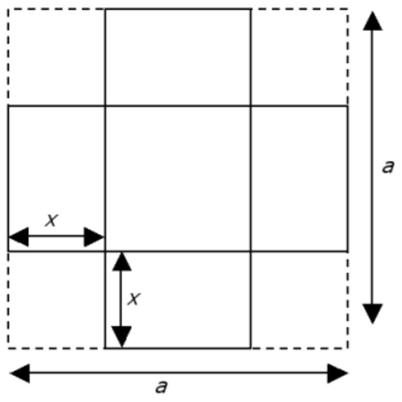 This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
 Here is another classic example of the three jug problem posed in the Mathigon Puzzle Calendars for 2017.
Here is another classic example of the three jug problem posed in the Mathigon Puzzle Calendars for 2017. This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.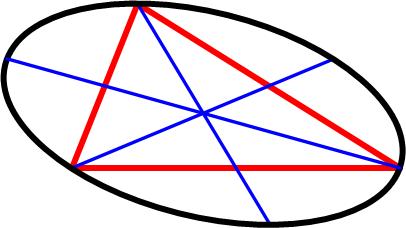 This is a tantalizing problem from the 1977 Crux Mathematicorum.
This is a tantalizing problem from the 1977 Crux Mathematicorum. This is a somewhat challenging problem from the 1997 American Invitational Mathematics Exam (AIME).
This is a somewhat challenging problem from the 1997 American Invitational Mathematics Exam (AIME).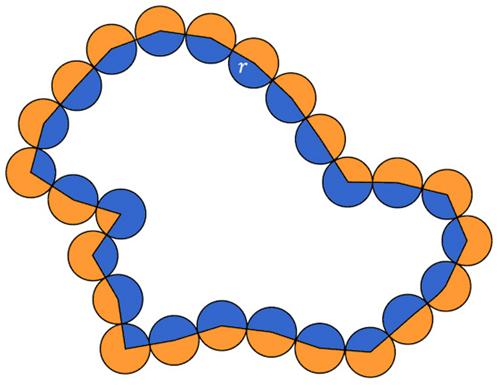 This is a nifty
This is a nifty  This is a fairly extensive clock problem by Geoffrey Mott-Smith from 1954.
This is a fairly extensive clock problem by Geoffrey Mott-Smith from 1954. This is a slightly challenging problem from Dan Griller.
This is a slightly challenging problem from Dan Griller. Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a
Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a  This essay is slightly tangential to my usual fare, but it is prompted by a most amazing video that convinced me that the impact of AI this time is not hype, but rather a real threat to our society. I found the
This essay is slightly tangential to my usual fare, but it is prompted by a most amazing video that convinced me that the impact of AI this time is not hype, but rather a real threat to our society. I found the