 Here is another elegant Quantum math magazine Brainteaser problem.
Here is another elegant Quantum math magazine Brainteaser problem.
“Two squares are inscribed in a semicircle as shown in the figure at left. Prove that the area of the big square is four times that of the small one.”

 Here is another elegant Quantum math magazine Brainteaser problem.
Here is another elegant Quantum math magazine Brainteaser problem.
“Two squares are inscribed in a semicircle as shown in the figure at left. Prove that the area of the big square is four times that of the small one.”
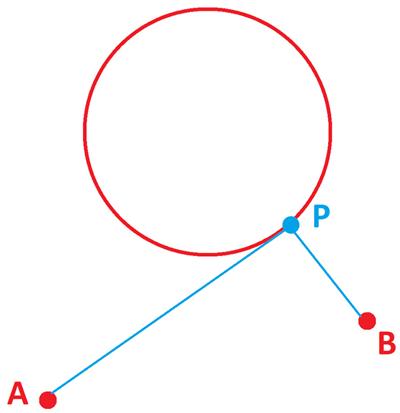 James Tanton provides another imaginative problem on Twitter.
James Tanton provides another imaginative problem on Twitter.
“I am at point A and want to walk to point B via some point, any point, P on the circle. What point P should I choose so that my journey A → P → B is as short as possible?”
Hint: I got ideas for a solution from two of my posts, “Square Root Minimum” and “Maximum Product”.
 This is a work problem from Geoffrey Mott-Smith from 1954.
This is a work problem from Geoffrey Mott-Smith from 1954.
“ ‘If a man can do a job in one day, how long will it take two men to do the job?’
No book of puzzles, I take it, is complete without such a question. I will not blame the reader in the least if he hastily turns the page, for I, too, was annoyed by “If a man” conundrums in my schooldays. Besides, the answer in the back of the book was always wrong. Everybody knows it will take the two men two days to do the job, because they will talk about women and the weather, they will argue about how the job is to be done, they will negotiate as to which is to do it. In schoolbooks the masons and bricklayers are not men, they are robots.
Strictly on the understanding that I am really talking about robots, I will put it to you:
If a tinker and his helper can refabulate a widget in 2 days, and if the tinker working with the apprentice instead would take 3 days, while the helper and the apprentice would take 6 days to do the job, how long would it take each working alone to refabulate the widget?”
See Refabulating Widgets for a solution.
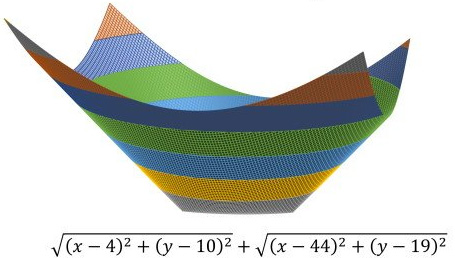 This seemingly impossible problem from Presh Talwalkar turned out to be quite solvable upon reflection.
This seemingly impossible problem from Presh Talwalkar turned out to be quite solvable upon reflection.
“A similar question was given to students in Thailand. For real numbers x, y, what is the minimum value of
√((x – 4)2 + (y – 10)2) + √((x – 44)2 + (y – 19)2)”
See the Square Root Minimum for solutions.
 This is a fun problem from the 1989 American Invitational Mathematics Exam (AIME).
This is a fun problem from the 1989 American Invitational Mathematics Exam (AIME).
“Two skaters, Allie and Billie, are at points A and B, respectively, on a flat, frozen lake. The distance between A and B is 100 meters. Allie leaves A and skates at a speed of 8 meters per second on a straight line that makes a 60° angle with AB. At the same time Allie leaves A, Billie leaves B at a speed of 7 meters per second and follows the straight path that produces the earliest possible meeting of the two skaters, given their speeds. How many meters does Allie skate before meeting Billie?”
See the Skating Rendezvous Problem for solutions.
 This puzzle from the Scottish Mathematical Council (SMC) Middle Mathematics Challenge has an interesting twist to it.
This puzzle from the Scottish Mathematical Council (SMC) Middle Mathematics Challenge has an interesting twist to it.
“Two young mountaineers were descending a mountain quickly at 6 miles per hour. They had left the hostel late in the day, had climbed to the top of the mountain and were returning by the same route. One said to the other “It was three o’clock when we left the hostel. I am not sure if we will be back before nine o’clock.” His companion replied “Our pace on the level was 4 miles per hour and we climbed at 3 miles per hour. We will just make it.” What is the total distance they would cover from leaving the hostel to getting back there?”
See the Mountain Climbing Puzzle for solutions.
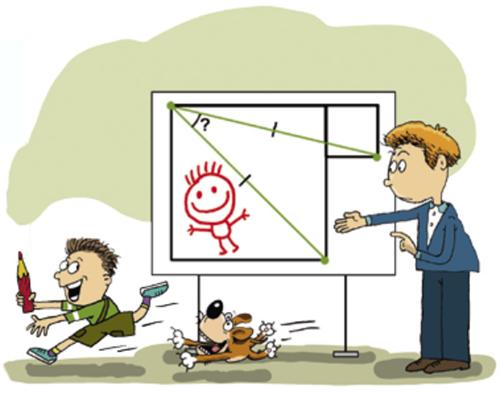 Via Alex Bellos I found another Russian math magazine with fun problems. It is called Kvantik and Tanya Khovanova has a description (2015):
Via Alex Bellos I found another Russian math magazine with fun problems. It is called Kvantik and Tanya Khovanova has a description (2015):
“Kvant [Quantum] was a very popular science magazine in Soviet Russia. It was targeted to high-school children and I was a subscriber. Recently I discovered that a new magazine appeared in Russia. It is called Kvantik, which means Little Kvant. It is a science magazine for middle-school children. The previous years’ archives are available online in Russian. I looked at 2012, the first publication year, and loved it.”
Unfortunately, the magazine is in Russian and the later issues are only partially given online. To get the full magazine you need to subscribe. I used Google Translate and the mathematical context to render the English. Here is an interesting geometric problem that I would have thought to be quite challenging for middle schoolers.
“The vertices of the two squares are joined by two segments, as in the figure. It is given that these segments are equal. Find the angle between them.
Egor Bakaev”
See the Two Squares Problem for a solution.
(Update 8/22/2022, 9/1/2022) Simpler Solution, Simplest Solution!
Continue reading
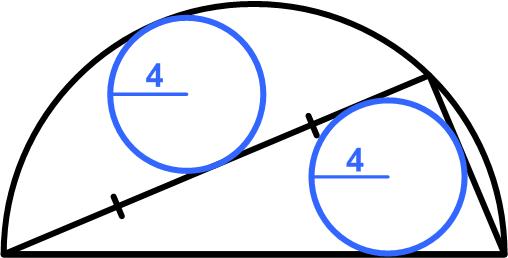 Here is a problem from the 2022 Math Calendar.
Here is a problem from the 2022 Math Calendar.
“Two small circles of radius 4 are inscribed in a large semicircle as shown. Find the radius of the large semicircle.”
As before, recall that all the answers are integer days of the month.
As seemed to be implied by the original Math Calendar diagram, I made explicit that the upper circle was tangent to the midpoint of the chord. Otherwise, the problem is insufficiently constrained.
See Two and a Half Circles for a solution.
 Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this Monday Puzzle from Alex Bellos in March is a timely reminder of the mathematical significance of that country.
Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this Monday Puzzle from Alex Bellos in March is a timely reminder of the mathematical significance of that country.
“Like many of you I’ve hardly been able to think about anything else these past ten days apart from the war in Ukraine. So today’s puzzles are a celebration of Lviv, Ukraine’s western city, which played an important role in the history of 20th century mathematics. During the 1930s, a remarkable group of scholars came up with new ideas, methods and theorems that helped shape the subject for decades.
The Lwów school of mathematics – at that time, the city was in Poland – was a closely-knit circle of Polish mathematicians, including Stefan Banach, Stanisław Ulam and Hugo Steinhaus, who made important contributions to areas including set-theory, topology and analysis. …
Of the many ideas introduced by the Lwów school, one of the best known is the “ham sandwich theorem,” posed by Steinhaus and solved by Banach using a result of Ulam’s. It states that it is possible to slice a ham sandwich in two with a single slice that cuts each slice of bread and the ham into two equal sizes, whatever the size and positions of the bread and the ham.
Today’s puzzles are also about dividing food. The first is from Hugo Steinhaus’ One Hundred Problems in Elementary Mathematics, published in 1938. The second uses a method involved in the proof of the ham sandwich theorem.
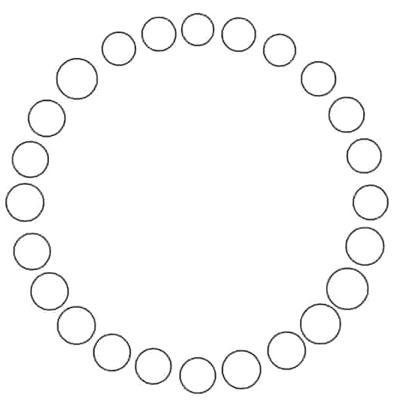
Show there is always a diameter that cuts the circle into two batches of 12 rolls with an equal number of plain and seeded.
Question 2 is adapted from Mathematical Puzzles by Peter Winkler, who gives as a reference Alon and West, The Borsuk-Ulam Theorem and bisection of necklaces, Proceedings of the American Mathematical Society 98 (1986).”
 I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age. I had read an essay of his in the New Yorker that turned out to be essentially excerpts from the book. I was so impressed with his descriptions of mathematics and intrigued by the premise of a mature adult in his 60s revisiting the nightmare of his high school experience with mathematics that I was eager to see if the book was as good as the essay. It was, and more.
I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age. I had read an essay of his in the New Yorker that turned out to be essentially excerpts from the book. I was so impressed with his descriptions of mathematics and intrigued by the premise of a mature adult in his 60s revisiting the nightmare of his high school experience with mathematics that I was eager to see if the book was as good as the essay. It was, and more.
The book is difficult to categorize—it is not primarily a history of mathematics, as suggested by Amazon. But it is fascinating on several levels. There is the issue of a mature perspective revisiting a period of one’s youth; the challenges of teaching a novice mathematics, especially a novice who has a strong antagonism for the subject; and insights into why someone would want to learn a subject that can be of no “use” to them in life, especially their later years.
Wilkinson has a strong philosophical urge; he wanted to understand the role of mathematics in human knowledge and the perspective it brought to life. He was constantly asking the big questions: is mathematics discovered or invented, what is the balance between nature and nurture, why does mathematics seem to describe the world so well, what is the link between memorization and understanding, how do you come to understand anything?