 This is a problem from the 629 AD work of Bhaskara I, a contemporary of Brahmagupta.
This is a problem from the 629 AD work of Bhaskara I, a contemporary of Brahmagupta.
“A fish is resting at the northeast corner of a rectangular pool. A heron standing at the northwest corner spies the fish. When the fish sees the heron looking at him he quickly swims towards the south (in a southwesterly direction rather than due south). When he reaches the south side of the pool, he has the unwelcome surprise of meeting the heron who has calmly walked due south along the side and turned at the southwest corner of the pool and proceeded due east, to arrive simultaneously with the fish on the south side. Given that the pool measures 12 units by 6 units, and that the heron walks as quickly as the fish swims, find the distance the fish swam.”
See Lunchtime at the Fish Pond for a solution.

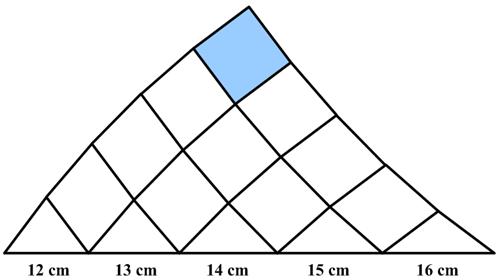 This is a
This is a 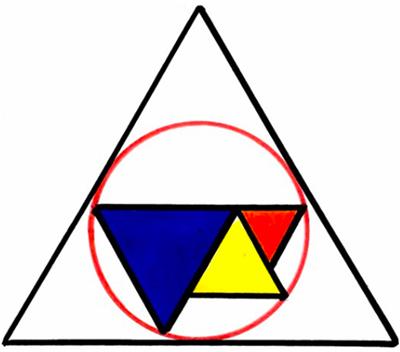 This is an old puzzle from Catriona Agg that I found on BL’s Math Games
This is an old puzzle from Catriona Agg that I found on BL’s Math Games  This is a
This is a  This is another nice problem from the 2025 Math Calendar.
This is another nice problem from the 2025 Math Calendar.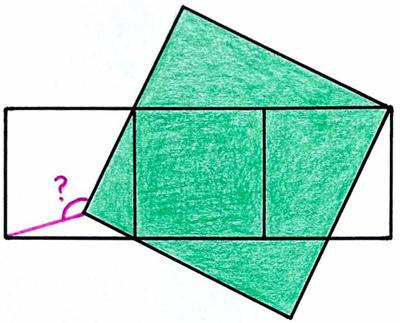 This is another Catriona Agg
This is another Catriona Agg  This is a lovely
This is a lovely 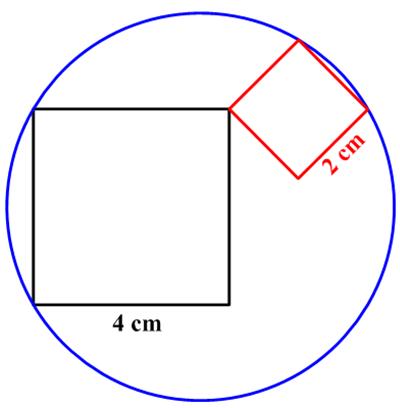 This
This 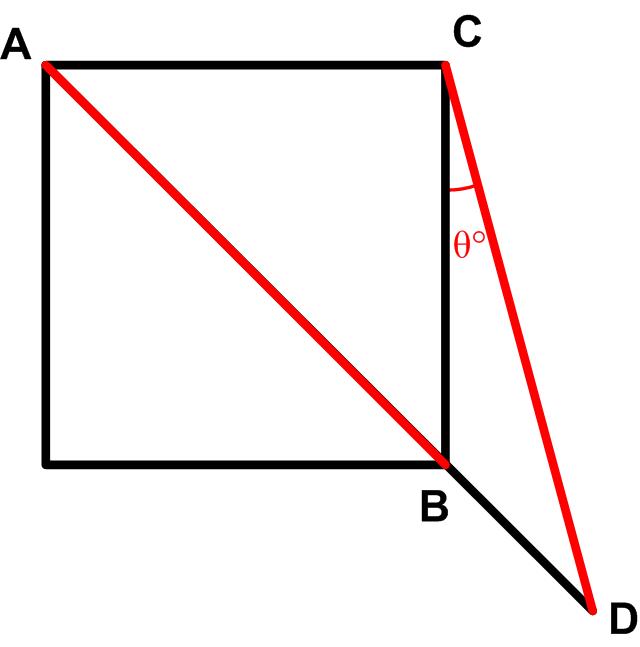 For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.
For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.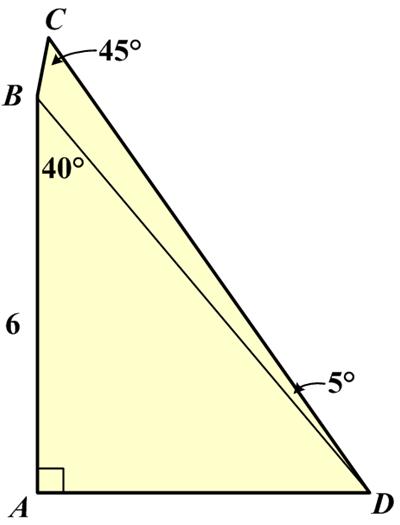 This is another intimidating
This is another intimidating