 Thanks to Futility Closet I discovered a new source of math puzzles: A+Click.
Thanks to Futility Closet I discovered a new source of math puzzles: A+Click.
“A+ Click helps students become problem solvers. Free, without ads, no calculators, and without signing-up. The website features a graduated set of 16,000+ challenging problems for students in grades one through twelve, starting from the very simple to the extremely difficult. … The questions concentrate on understanding, spatial reasoning, usefulness, and problem solving rather than math rules and theorems. The problems include a short description and an illustration to help problem solvers visualize the model. The problems can be solved within one minute and without using a calculator.”
My only quibble with “The questions concentrate on understanding, spatial reasoning, usefulness, and problem solving rather than math rules and theorems.” is that by keeping explicit math notation and concepts to a minimum, the use of symbolic algebra and calculus is muted and there is a whiff of the medieval reliance on mental verbal agility rather than the power of the new mathematics.
Still the problems are imaginative and challenging. Here is a good example.
“The rear tires of my car wear out after 40,000 miles, while the front tires are done after 20,000 miles. Estimate how many miles I should drive before the tires (front and rear) are rotated to drive the maximal distance.
Answer Choices: 15,000 miles 12,000 miles 13,333 miles 16,667 miles”
(I admit solving these under a minute is a challenge, at which I often failed. Ignoring time constraints allows for greater care and a more thorough mulling over the intricacies of the problem. Yes, those who have mastered math can solve problems faster than those who have not, but real mastery of math requires an inordinate attention to details, and that requires time.)
Answer.
See Tire Wear for solutions.
 This is an interesting problem from the Canadian Mathematical Society’s 2001 Olymon.
This is an interesting problem from the Canadian Mathematical Society’s 2001 Olymon.
 Thanks to Futility Closet I discovered a new source of math puzzles:
Thanks to Futility Closet I discovered a new source of math puzzles:  This is another simple problem from the 2025 Math Calendar.
This is another simple problem from the 2025 Math Calendar. This is a puzzle from
This is a puzzle from  This is another
This is another  Presh Talwalkar has an interesting new
Presh Talwalkar has an interesting new 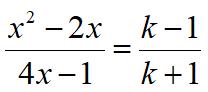 ”
” This is a nice problem from Five Hundred Mathematical Challenges.
This is a nice problem from Five Hundred Mathematical Challenges. This is a 2017 Center of Mathematics Problem of the Week.
This is a 2017 Center of Mathematics Problem of the Week. This is an interesting algebra
This is an interesting algebra 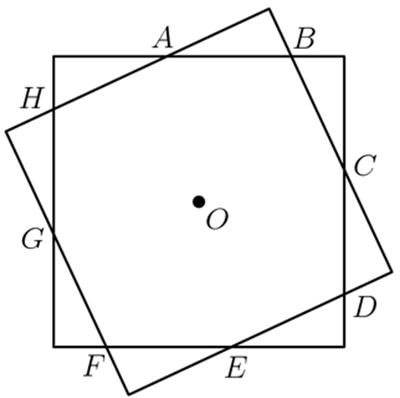 This is a fairly straight-forward problem from the 1999 AIME problems.
This is a fairly straight-forward problem from the 1999 AIME problems.