This is a rather mind-boggling problem from the 1947 Eureka magazine.
This is a rather mind-boggling problem from the 1947 Eureka magazine.
“Six men, A, B, C, D, E, F, of negligible honesty, met on a perfectly rough day, each carrying a light inextensible umbrella. Each man brought his own umbrella, and took away—let us say “borrowed”—another’s. The umbrella borrowed by A belonged to the borrower of B’s umbrella. The owner of the umbrella borrowed by C borrowed the umbrella belonging to the borrower of D’s umbrella. If the borrower of E’s umbrella was not the owner of that borrowed by F, who borrowed A’s umbrella?”
See the Umbrella Problem for solutions.

 This is a nice little puzzle from the 2024 Math Calendar.
This is a nice little puzzle from the 2024 Math Calendar.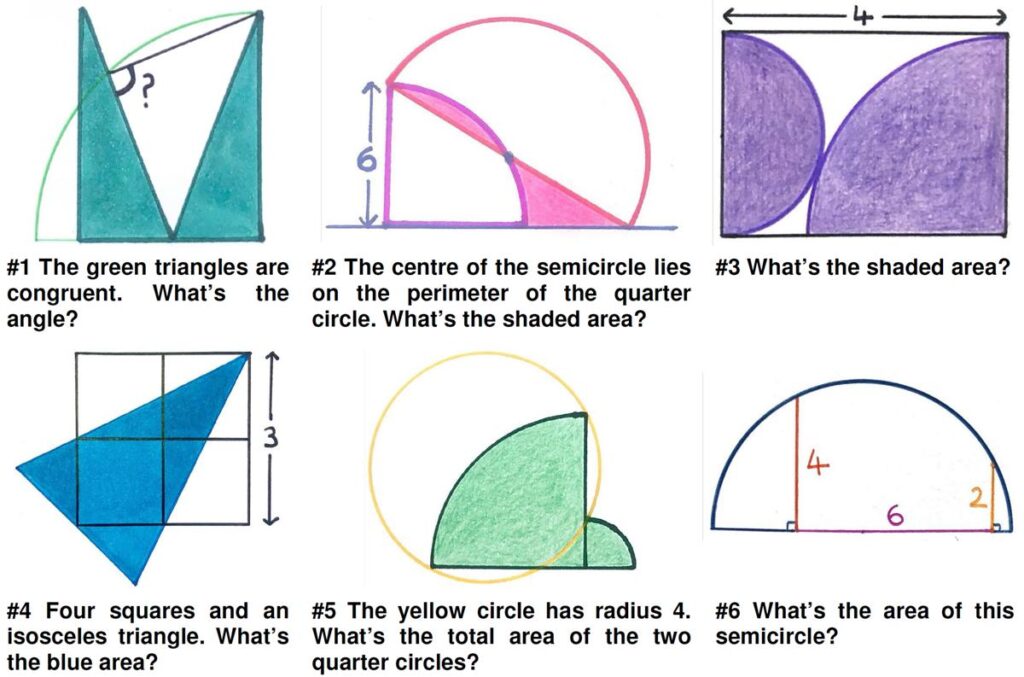
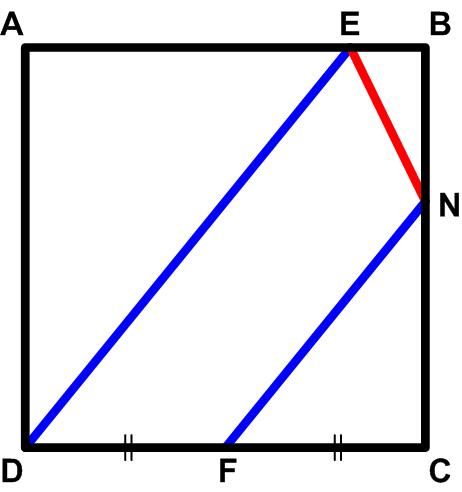 This is an interesting problem from the collection Five Hundred Mathematical Challenges.
This is an interesting problem from the collection Five Hundred Mathematical Challenges. This is a challenging problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website.
This is a challenging problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website. This is an interesting problem from 180 BC China.
This is an interesting problem from 180 BC China. I came across this remarkable
I came across this remarkable  Coming across this
Coming across this  This is a clever puzzle from the 1986 AIME problems.
This is a clever puzzle from the 1986 AIME problems. This is an intriguing
This is an intriguing