 This is an interesting problem from the 1966 Eureka magazine.
This is an interesting problem from the 1966 Eureka magazine.
“A railway and a road run together for seven miles from P to Q. Two miles from P there is a level crossing, which is closed one minute before, and opened one minute after, a train passes.
A train passes a Stationary car at P and travels on to Q at 60 m.p.h., and, forgetting to slow down, crashes at Q; the car passes the train as it crashes. Assuming that stopping for an instant from full speed loses the car one minute, of what speed must it be capable?”
See the Railway Crossing Problem for a solution.

 This is a classic
This is a classic 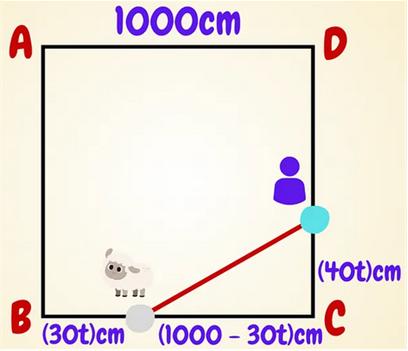 This is a slightly challenging
This is a slightly challenging  This is a
This is a  This is another nice problem from the 2025 Math Calendar.
This is another nice problem from the 2025 Math Calendar.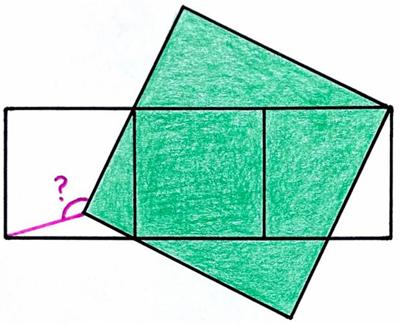 This is another Catriona Agg
This is another Catriona Agg  This is another take on the passing train type puzzle from the Moscow Puzzles.
This is another take on the passing train type puzzle from the Moscow Puzzles. This is a lovely
This is a lovely 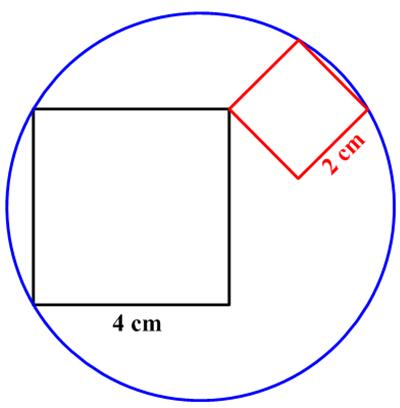 This
This  Here is a probability
Here is a probability