 This is another challenging sum from the 2024 Math Calendar.
This is another challenging sum from the 2024 Math Calendar.
“Find x where x = et and
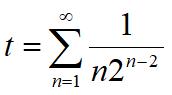 ”
”
As before, recall that all the answers are integer days of the month.
See Yet Another Sum for a solution.

 This is another challenging sum from the 2024 Math Calendar.
This is another challenging sum from the 2024 Math Calendar.
“Find x where x = et and
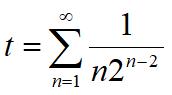 ”
”
As before, recall that all the answers are integer days of the month.
See Yet Another Sum for a solution.
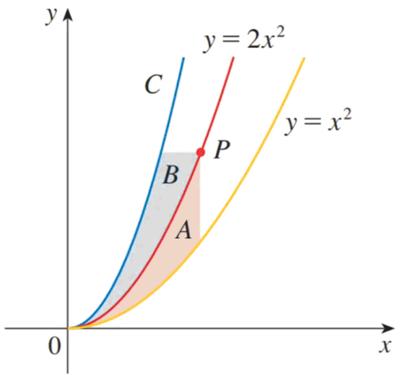 Here is another problem from BL’s Weekly Math Games.
Here is another problem from BL’s Weekly Math Games.
“For every point P on y = 2x2, areas A and B are equal. Find the equation for curve C.”
See Mystery Curve Puzzle for a solution
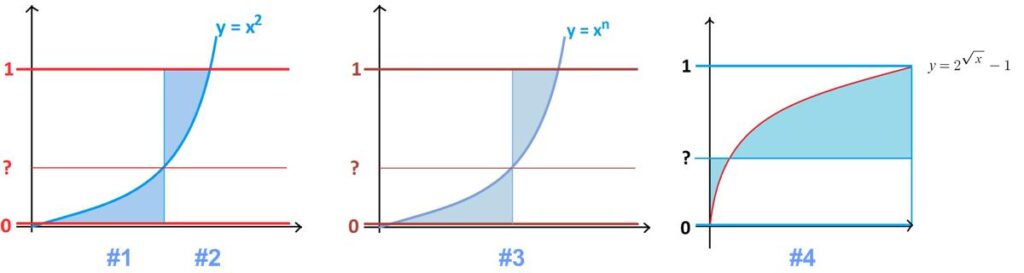 A while ago James Tanton provided a series of puzzles:
A while ago James Tanton provided a series of puzzles:
Puzzle #1 At what value between 0 and 1 does a horizontal line at that height produce two regions of equal area as shown on the graph of y = x2?
Puzzle #2 A horizontal line is drawn between the lines y = 0 and y = 1, dividing the graph of y = x2 into two regions as shown. At what height should that line be drawn so that the sum of the areas of these two regions is minimal?
Puzzle #3 A horizontal line is drawn between the lines y = 0 and y = 1, dividing the graph of y = xn into two regions as shown (n > 0). At what height should that line be drawn so that the sum of the areas of these two regions is minimal? Does that height depend on the value of n?
Puzzle #4 What horizontal line drawn between y = 0 and y = 1 on the graph of y = 2√x – 1 minimizes the sum of the two shaded areas shown?
See Double Areas Puzzles for solutions.
 This is another puzzle from BL’s Weekly Math Games.
This is another puzzle from BL’s Weekly Math Games.
“a + b + c = 2, and
a2 + b2 + c2 = 12
where a, b, and c are real numbers. What is the difference between the maximum and minimum possible values of c?”
The original problem statement mentioned a fourth real number d, but I considered it a typo, since it was not involved in the problem.
See Sphere and Plane Puzzle for a solution.
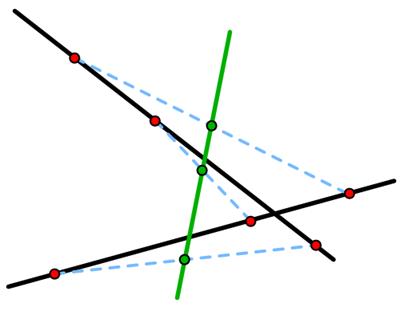 I came across this remarkable result in Futility Closet:
I came across this remarkable result in Futility Closet:
“On each of these two black lines is a trio of red points marked by the same distances. The midpoints of segments drawn between corresponding points are collinear.
(Discovered by Danish mathematician Johannes Hjelmslev.)”
This result seems amazing and mysterious. I wondered if I could think of a proof. I found a simple approach that did not use plane geometry. And suddenly, like a magic trick exposed, the result seemed obvious.
 Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
_______________
As before, recall that all the answers are integer days of the month.
See the Amazing Root Problem for a solution.
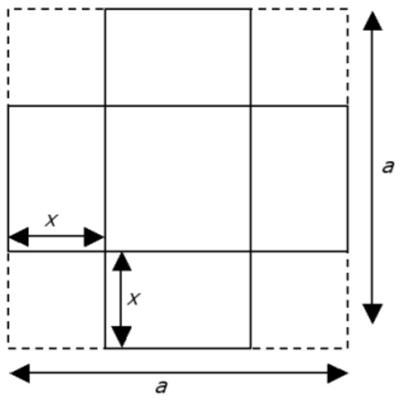 This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
“Four corners measuring x by x are removed from a sheet of material that measures a by a to make a square based open-top box. Prove that the volume of the box is maximised iff the area of the base is equal to the area of the four sides.”
See the Maximized Box Problem
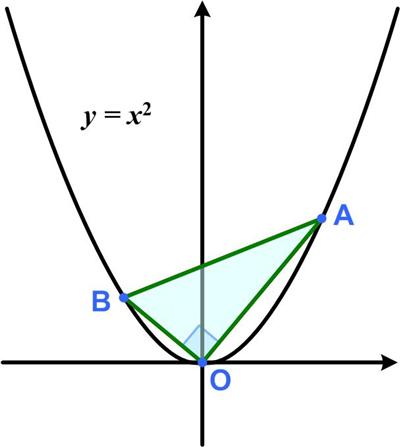 Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a post from 10 May 2021 that I had not seen before, namely,
Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a post from 10 May 2021 that I had not seen before, namely,
“The points A and B are on the curve y = x2 such that AOB is a right angle. What points A and B will give the smallest possible area for the triangle AOB?”
See the Pythagorean Parabola Puzzle for solution.
(Update 9/1/2023) Elegant Alternative Solution by Oscar Rojas
Continue reading
 Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem.
Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem.
“A cyclist sets off from point O and rides with constant velocity v along a rectilinear highway. A messenger, who is at a distance a from point O and at a distance b from the highway, wants to deliver a letter to the cyclist. What is the minimum velocity with which the messenger should run in order to attain his objective?”
See the Tired Messenger Problem
(Update 1/29/2025) Dan Steinitz Solution
Dan Steinitz from Israel has sent an elegant solution that only involves vectors and geometry without calculus. I have edited slightly his email and added excerpts from his whiteboard solution, though without the Hebrew annotations, which unfortunately I cannot read. But that is the glory of the universal language of mathematics: it can be read and understood in any language.
 This is another physics-based problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) that may take a bit more thought.
This is another physics-based problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) that may take a bit more thought.
“A firework rocket is fired vertically upwards with a constant acceleration of 4 m/s2 until the chemical fuel expires. Its ascent is then slowed by gravity until it reaches a maximum height of 138 metres.
Assuming no air resistance and taking g = 9.8 m/s2, how long does it take to reach its maximum height?”
I can never remember the formulas relating acceleration, velocity, and distance, so I always derive them via integration.
See the Fireworks Rocket for solutions.