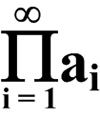This is a challenging problem from Mathematical Quickies (1967).
“Evaluate the infinite product:
”
I came up with a motivated solution using some standard techniques from calculus. Mathematical Quickies had a solution that did not employ calculus, but one which I felt used unmotivated tricks.
See the Infinite Product Problem for solutions.
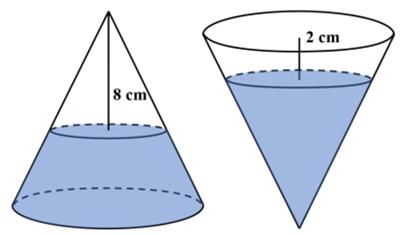I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.
Presh Talwalkar: “This was sent to me as a competition problem for 8th graders, so it would be a challenge problem for students aged 12 to 13. When a conical bottle rests on its flat base, the water in the bottle is 8 cm from its vertex. When the same conical bottle is turned upside down, the water level is 2 cm from its base. What is the height of the bottle? (Note “conical” refers to a right circular cone as is common usage.) I at first thought this problem was impossible. But it actually can be solved.”
See the Conical Bottle Problem for solutions.
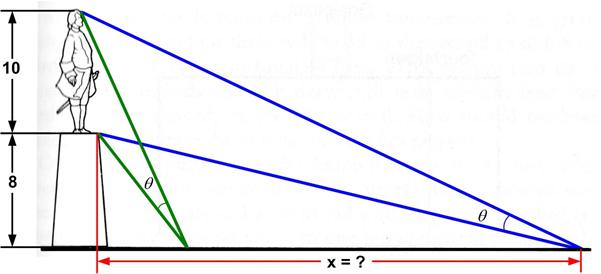This is an old problem I had seen before. Here is David Wells’s rendition:
“Johannes Müller, named Regiomontanus after the Latin translation of Körnigsberg, his city of birth, later made famous by Euler, proposed this problem in 1471. … it is usually put in this form …: From what distance will a statue on a plinth appear largest to the eye [of a mouse!]? If we approach too close, the statue appears foreshortened, but from a distance it is simply small.”
I have added height numbers in feet for concreteness (as well as the mouse qualification, since the angles are measured from ground level). So the problem is to find the distance x such that the angle is maximal.
See the Regiomontanus 1471 Problem for solutions.
The following interesting behavior was found at the Futility Closet website:
“A pleasing fact from David Wells’ Archimedes Mathematics Education Newsletter: Draw two parallel lines. Fix a point A on one line and move a second point B along the other line. If an equilateral triangle is constructed with these two points as two of its vertices, then as the second point moves, the third vertex C of the triangle will trace out a straight line. Thanks to reader Matthew Scroggs for the tip and the GIF.”
This is rather amazing and cries out for a proof. It also raises the question of how anyone noticed this behavior in the first place. I proved the result with calculus, but I wonder if there is a slicker way that makes it more obvious. See the Straight and Narrow Problem.
(Update 3/25/2019) Continue reading
I came across the following problem from an Italian high school exam on the British Aperiodical website presented by Adam Atkinson:
“There have been various stories in the Italian press and discussion on a Physics teaching mailing list I’m accidentally on about a question in the maths exam for science high schools in Italy last week. The question asks students to confirm that a given formula is the shape of the surface needed for a comfortable ride on a bike with square wheels.
What do people think? Would this be a surprising question at A-level in the UK or in the final year of high school in the US or elsewhere?”
I had seen videos of riding a square-wheeled bicycle over a corrugated surface before, but I had never inquired about the nature of the surface. So I thought it would be a good time to see if I could prove the surface (cross-section) shown would do the job. See Square Wheels.
(Update 9/14/2023) Square Bridge That Rolls!
This is an incredible application of the rolling square wheels idea described on Matt Parker’s Stand-up Maths Youtube website. It also demonstrates the difference between engineering and pure math. The engineers had to solve some challenging problems to adapt the theoretical math to a practical application. And such solutions are always required under tight time constrictions. Engineering certainly is a noble profession.
These are three “Coffin” Problems posed by Nakul Dawra on his Youtube site GoldPlatedGoof. (Nakul is extraordinarily entertaining and mesmerizing.) The origin of the name is explained, but basically they are problems that have easy or even trivial solutions—once you see the solution. But just contemplating the problem, they seem impossible. The idea was to kill the chances of the pupil taking an (oral) exam with these problems. I was able to solve the first two problems (after a while), but I could not figure out the third. See the Three Coffin Problems.
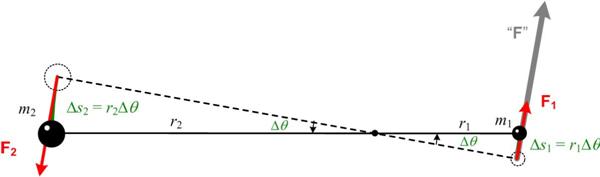I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his “equal areas law” and Newton’s elegant geometric proof. I love the fact that a simple geometric argument, seemingly totally divorced from the physical situation, can provide an explanation for why the line from the Sun to a planet sweeps out equal areas in equal time as the planet orbits the Sun, solely under the influence of the gravitational force between them. However, modern physics books invariably cite the conservation of angular momentum as the “explanation.” I indicated before in my “Kepler’s Laws and Newton’s Laws” essay that this “explanation” irritated me. In this essay I go into detail about my reservations concerning this line of argument. See Angular Momentum.
This may be a futile attempt at an elementary introduction to complex variables by emphasizing their geometric properties. The elementary part is probably undermined by an initial discussion of field extensions and a necessary reference to trigonometry. Hopefully, the suppression of the explicit use of complex powers of Euler’s constant e until the very end will allow the geometric ideas to have center stage. A primary goal of the essay is to realize that complex polynomials involve sums of circles in the plane. The image of real polynomials as wavy curves in the plane is misleading for an understanding of complex behavior. See Complex Numbers – Geometric Viewpoint.
I found this collection of related problems by James Tanton on Twitter. Even though all these problems do not involve perpendiculars, they have a common solution approach – a sort of theme and variations idea. In a later tweet Tanton refers to a Viviani Theorem associated with these types of problems. I did not recall that theorem explicitly or by name. I also have not looked it up yet, in order to solve these problems on my own. I am guessing there is a more classical Euclidean geometry proof, but I like my vector approach for its clarity. I also throw in a bit a calculus at the end for fun. See Polygon Altitude Problems I
A number of recent puzzles have involved perspective views of objects. I had never really explored the idea of a perspective map in detail. So some of the properties associated with it always seemed a bit vague to me. I decided I would derive the mathematical equations for the perspective or projective map and see how its properties fell out from the equations. With this information in hand I then addressed some questions I had about the article “Dürer: Disguise, Distance, Disagreements, and Diagonals!” by Annalisa Crannell, Marc Frantz, and Fumiko Futamura concerning a controversy over Albrecht Dürer’s woodcut St. Jerome in His Study (1514). And finally, I read somewhere that a parabola under a perspective map becomes an ellipse, so I was able to show that as well. See the Perspective Map.
(Update 7/1/2019) Continue reading
