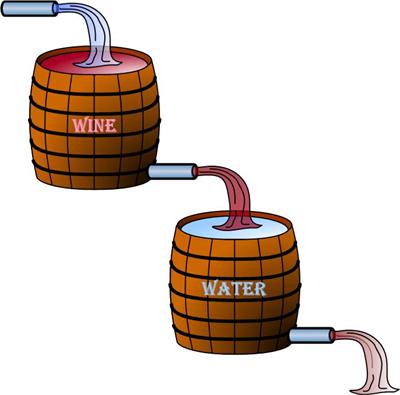
 Here is a challenging problem from the 1874 The Analyst.
Here is a challenging problem from the 1874 The Analyst.
“A cask containing a gallons of wine stands on another containing a gallons of water; they are connected by a pipe through which, when open, the wine can escape into the lower cask at the rate of c gallons per minute, and through a pipe in the lower cask the mixture can escape at the same rate; also, water can be let in through a pipe on the top of the upper cask at a like rate. If all the pipes be opened at the same instant, how much wine will be in the lower cask at the end of t minutes, supposing the fluids to mingle perfectly?
— Communicated by Artemas Martin, Mathematical Editor of Schoolday Magazine, Erie, Pennsylvania.”
I found the problem in Benjamin Wardhaugh’s book where he describes The Analyst:
“Beginning in 1874 and continuing as Annals of Mathematics from 1884 onward, The Analyst appeared monthly, published in Des Moines, Iowa, and was intended as “a suitable medium of communication between a large class of investigators and students in science, comprising the various grades from the students in our high schools and colleges to the college professor.” It carried a range of mathematical articles, both pure and applied, and a regular series of mathematical problems of varying difficulty: on the whole they seem harder than those in The Ladies’ Diary and possibly easier than the Mathematical Challenges in the extract after the next. Those given here appeared in the very first issue.”
I tailored my solution after the “Diluted Wine Puzzle”, though this problem was more complicated. Moreover, the final solution must pass from discreet steps to continuous ones.
There is a bonus problem in a later issue:
“19. Referring to Question 4, (No. 1): At what time will the lower cask contain the greatest quantity of wine?
—Communicated by Prof. Geo. R. Perkins.”
Answer.
See the Wine Into Water Problem for solutions.
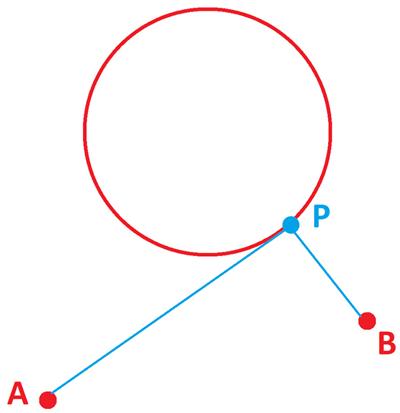 James Tanton provides another imaginative problem on Twitter.
James Tanton provides another imaginative problem on Twitter.
 I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age. I had read an
I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age. I had read an  Here is another sum problem, this time from the 2021 Math Calendar.
Here is another sum problem, this time from the 2021 Math Calendar. Here is a challenging problem from the 1874 The Analyst.
Here is a challenging problem from the 1874 The Analyst. I thought it might be interesting to explore the mathematics of a common problem with a store-bought HO model train set that contains a collection of straight track segments and fixed-radius curved track segments that form a simple oval. Invariably an initial run of the train has it careening off the track when the train first meets the curved segment after running along the straight track segments.
I thought it might be interesting to explore the mathematics of a common problem with a store-bought HO model train set that contains a collection of straight track segments and fixed-radius curved track segments that form a simple oval. Invariably an initial run of the train has it careening off the track when the train first meets the curved segment after running along the straight track segments. Here is another problem from the 2020 Math Calendar.
Here is another problem from the 2020 Math Calendar.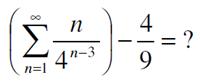
 The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto. The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university.
The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto. The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university.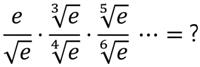 This is a delightful and surprising problem from
This is a delightful and surprising problem from  If you will pardon the pun, this is a diabolical problem from the collection Five Hundred Mathematical Challenges.
If you will pardon the pun, this is a diabolical problem from the collection Five Hundred Mathematical Challenges. Here is another Brain Bogglers problem from 1987.
Here is another Brain Bogglers problem from 1987.