 Alcuin of York (735-804) had a series of similar problems involving the distribution of corn among servants. Since the three propositions were the same format with only the numbers changing, I thought I would present them in a more concise form:
Alcuin of York (735-804) had a series of similar problems involving the distribution of corn among servants. Since the three propositions were the same format with only the numbers changing, I thought I would present them in a more concise form:
“Proposition
A certain head of household had a number of servants, consisting of men, women, and children, among whom he wished to distribute quantities, modia, of corn. The men should receive three modia; the women, two; and the children, half a modium.
(a) If the head of household has 20 servants and wished to distribute 20 modia of corn among them, let him say, he who can, How many men, women and children must there have been.
(b) If the head of household has 30 servants and wished to distribute 30 modia of corn among them, let him say, he who can, How many men, women and children must there have been.
(c) If the head of household has 100 servants and wished to distribute 100 modia of corn among them, let him say, he who can, How many men, women and children must there have been.”
I will give Alcuin’s solutions first, followed by my more expansive solutions that rely on our familiar symbolic algebra that was not available in Alcuin’s time.
See Alcuin’s Corn Problem
Post Views: 184
 This is another physics-based problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) that may take a bit more thought.
This is another physics-based problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) that may take a bit more thought.
 This is a fun logic
This is a fun logic  Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine. Alcuin of York (735-804) had a series of similar problems involving the distribution of corn among servants. Since the three propositions were the same format with only the numbers changing, I thought I would present them in a more concise form:
Alcuin of York (735-804) had a series of similar problems involving the distribution of corn among servants. Since the three propositions were the same format with only the numbers changing, I thought I would present them in a more concise form: This is a classic type of puzzle from Henry Dudeney.
This is a classic type of puzzle from Henry Dudeney.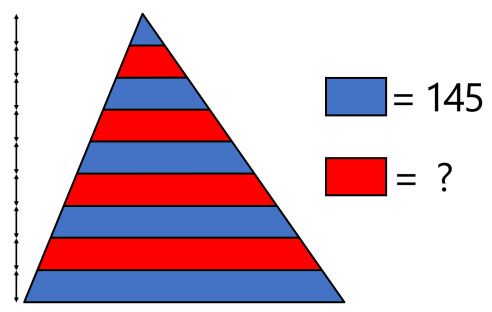 This is a fairly straight-forward problem from Presh Talwalkar.
This is a fairly straight-forward problem from Presh Talwalkar.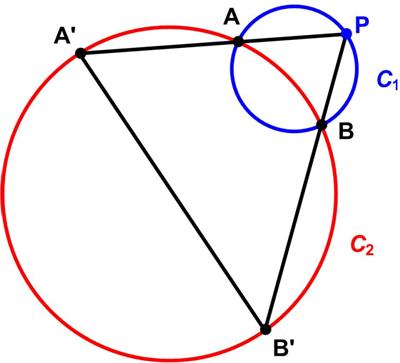 This is a Maths Item of the Month (MIOM)
This is a Maths Item of the Month (MIOM) 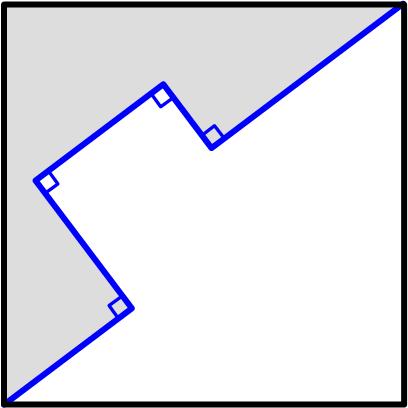 This is a nice problem from the UKMT Senior Mathematics Challenge for 2022:
This is a nice problem from the UKMT Senior Mathematics Challenge for 2022: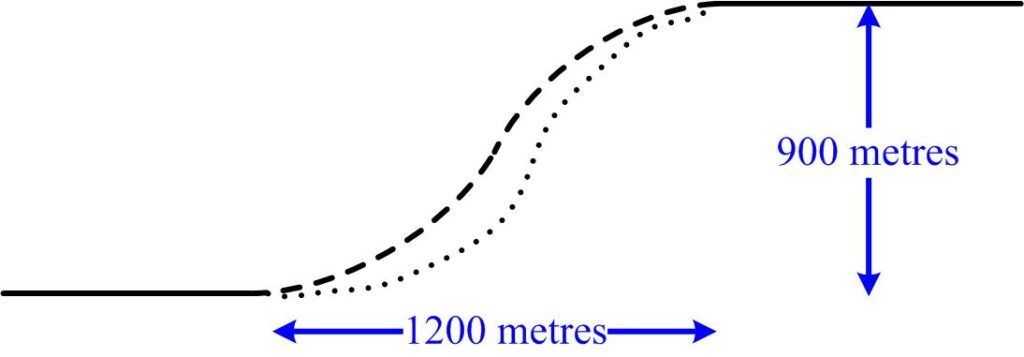 This is an interesting problem from the Scottish Mathematics Council (SMC) 2014 Senior Math Challenge .
This is an interesting problem from the Scottish Mathematics Council (SMC) 2014 Senior Math Challenge . This is another stimulating little problem from the 2022 Math Calendar.
This is another stimulating little problem from the 2022 Math Calendar.