 Here is another Brainteaser from the Quantum math magazine.
Here is another Brainteaser from the Quantum math magazine.
“Nick left Nicktown at 10:18 A.M. and arrived at Georgetown at 1:30 P.M., walking at a constant speed. On the same day, George left Georgetown at 9:00 A.M. and arrived at Nicktown at 11:40 A.M., walking at a constant speed along the same road. The road crosses a wide river. Nick and George arrived at the bridge simultaneously, each from his side of the river. Nick left the bridge 1 minute later than George. When did they arrive at the bridge?”
See Meeting on the Bridge for solutions.

 Here is a tricky little logarithm problem from the 2021 Math Calendar.
Here is a tricky little logarithm problem from the 2021 Math Calendar. This is an imaginative puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2012.
This is an imaginative puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2012.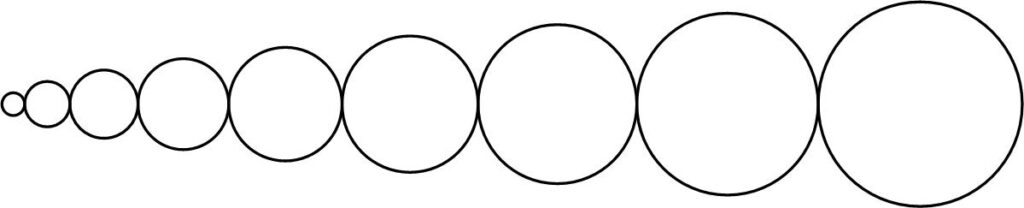
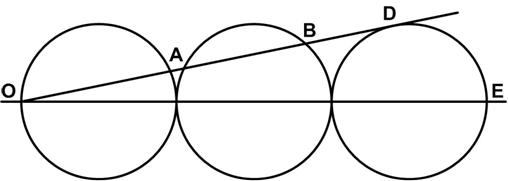 This is a straight-forward problem by Geoffrey Mott-Smith from 1954.
This is a straight-forward problem by Geoffrey Mott-Smith from 1954. This is another candle burning problem, presented by
This is another candle burning problem, presented by 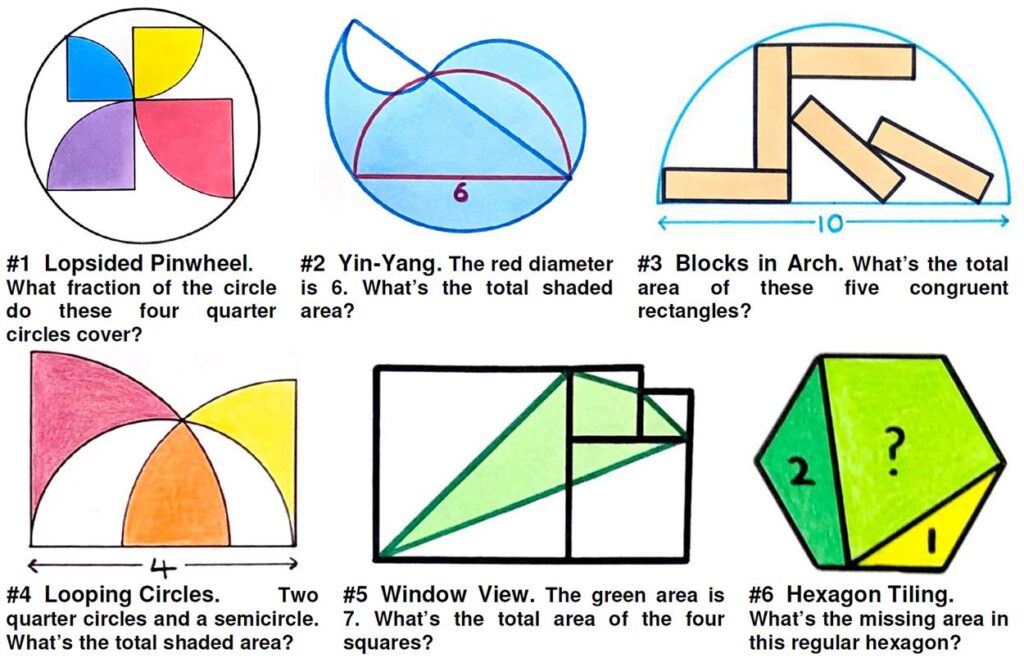 Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer).
Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer). This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2007:
This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2007: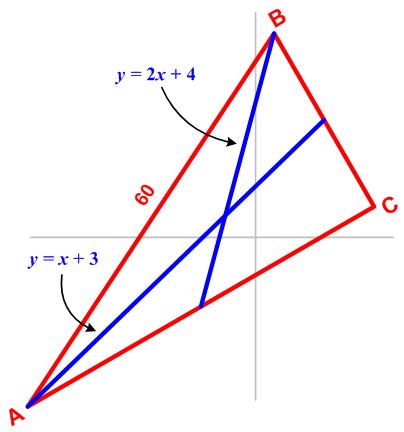 This is a challenging problem from the 1986 American Invitational Mathematics Exam (AIME).
This is a challenging problem from the 1986 American Invitational Mathematics Exam (AIME). Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov.
Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov.