
This is from the UKMT Senior Challenge of 1999.
What is the sum to infinity of the convergent series![]()
A_7/4_____B_2_____C_√5_____D_9/4_____E_7/3”
See Fibonacci Fandango for a solution.


This is from the UKMT Senior Challenge of 1999.
What is the sum to infinity of the convergent series![]()
A_7/4_____B_2_____C_√5_____D_9/4_____E_7/3”
See Fibonacci Fandango for a solution.
 This is a great posting by the mathematician James Propp on his website Mathematical Enchantments, not only for the main story about his experience as a mathematician at a trial, but also for his short excursion into the idea of definitions in mathematics—basically the same topic I was trying to address in my posts on “A Meditation on ‘Is’ in Mathematics” here and here.
This is a great posting by the mathematician James Propp on his website Mathematical Enchantments, not only for the main story about his experience as a mathematician at a trial, but also for his short excursion into the idea of definitions in mathematics—basically the same topic I was trying to address in my posts on “A Meditation on ‘Is’ in Mathematics” here and here.
Normally I would excerpt such an article and provide the link to the full article, but given the short half-life of links I have also provided a full PDF copy just in case. You should visit the link to see the comments, which I have not included (Propp is lucky to have some of those). In fact, you should take the opportunity to peruse a number of his articles, if you have not already, which are longer in nature, appear monthly, and provide some great insights into mathematics (his pseudosphere icon is the Beltrami surface, which he discusses elsewhere).
 This is a tricky product problem from Alfred Posamentier which naturally has a slick solution—if you can think of it.
This is a tricky product problem from Alfred Posamentier which naturally has a slick solution—if you can think of it.
“Find the numerical value of the following expression:![]()
“_
See A Tricky Product for a solution.
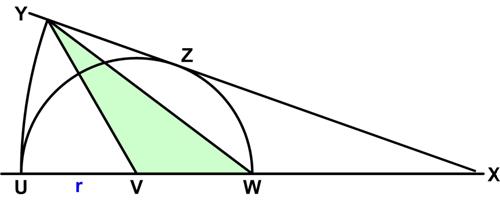 Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:
Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:
“A semicircle of radius r is drawn with centre V and diameter UW. The line UW is then extended to the point X, such that UW and WX are of equal length. An arc of the circle with centre X and radius 4r is then drawn so that the line XY is tangent to the semicircle at Z, as shown. What, in terms of r, is the area of triangle YVW?”
See the Rising Sun for solutions.
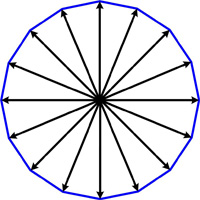 This is a fun problem from Mathematical Quickies (1967).
This is a fun problem from Mathematical Quickies (1967).
“Prove that the sum of the vectors from the center of a regular polygon of n sides to its vertices is zero.”
See the Vector Sum Problem.
 This is another UKMT Senior Challenge problem, but for the year 2005. I thought it was diabolical and hadn’t a clue how to solve it. Even after reading the solution, I don’t think I could have come up with it. I take my hat off to anyone who solves it.
This is another UKMT Senior Challenge problem, but for the year 2005. I thought it was diabolical and hadn’t a clue how to solve it. Even after reading the solution, I don’t think I could have come up with it. I take my hat off to anyone who solves it.
“Which of the following is equal to
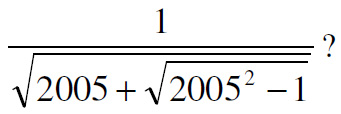
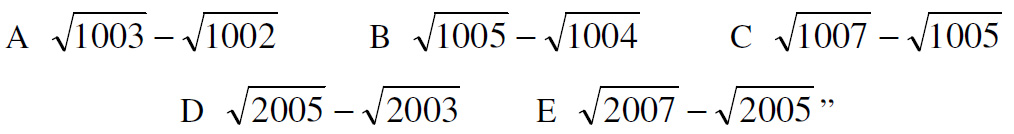
See Radical Radicals for a solution.
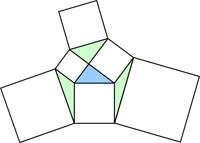 This is a problem from the UKMT Senior Challenge for 2001. (It has been slightly edited to reflect the colors I added to the diagram.)
This is a problem from the UKMT Senior Challenge for 2001. (It has been slightly edited to reflect the colors I added to the diagram.)
“The [arbitrary] blue triangle is drawn, and a square is drawn on each of its edges. The three green triangles are then formed by drawing their lines which join vertices of the squares and a square is now drawn on each of these three lines. The total area of the original three squares is A1, and the total area of the three new squares is A2. Given that A2 = k A1, then
_____A_ k = 1_____B_ k = 3/2_____C_ k = 2_____D_ k = 3_____E_ more information is needed.”
I solved this problem using a Polya principle to simplify the situation, but UKMT’s solution was direct (and more complicated).
See the Six Squares Problem for solutions.
 Yet another train problem from H. E. Dudeney.
Yet another train problem from H. E. Dudeney.
“We were going by train from Anglechester to Clinkerton, and an hour after starting an accident happened to the engine. We had to continue the journey at three-fifths of the former speed. It made us two hours late at Clinkerton, and the driver said that if only the accident had happened fifty miles farther on the train would have arrived forty minutes sooner. Can you tell from that statement just how far it is from Anglechester to Clinkerton?”
See the Damaged Engine for a solution.
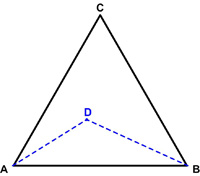 Catriona Shearer retweeted the following problem from Antonio Rinaldi @rinaldi6109
Catriona Shearer retweeted the following problem from Antonio Rinaldi @rinaldi6109
“My little contribution to @Cshearer41 October 7, 2018
A point D is randomly chosen inside the equilateral triangle ABC. Determine the probability that the triangle ABD is acute-angled.”
See Triangle Acute-Angle Problem for a solution.
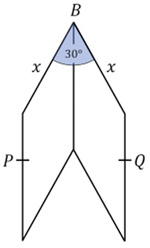 Another challenging problem from Presh Talwalkar. I certainly could not have solved it on a timed test at the age of 16.
Another challenging problem from Presh Talwalkar. I certainly could not have solved it on a timed test at the age of 16.
“One Of The Hardest GCSE Test Questions – How To Solve The Cosine Problem
Construct a hexagon from two congruent parallelograms as shown. Given BP = BQ = 10, solve for the cosine of PBQ in terms of x.
This comes from the 2017 GCSE exam, and it confused many people. I received many requests to solve this problem, and I thank Tom, Ben, and James for suggesting it to me.”
See the Parallelogram Cosine Problem for solutions.