 This interesting problem comes from Colin Hughes at the Maths Challenge website.
This interesting problem comes from Colin Hughes at the Maths Challenge website.
“Problem
Prove that for any number that is not a multiple of seven, then its cube will be one more or one less than a multiple of 7.”
See Lucky 7 Problem

 This interesting problem comes from Colin Hughes at the Maths Challenge website.
This interesting problem comes from Colin Hughes at the Maths Challenge website.
“Problem
Prove that for any number that is not a multiple of seven, then its cube will be one more or one less than a multiple of 7.”
See Lucky 7 Problem
 A glutton for punishment I considered another Sam Loyd puzzle:
A glutton for punishment I considered another Sam Loyd puzzle:
“Three men had a tandem and wished to go just forty miles. It could complete the journey with two passengers in one hour, but could not carry the three persons at one time. Well, one who was a good pedestrian, could walk at the rate of a mile in ten minutes; another could walk in fifteen minutes, and the other in twenty. What would be the best possible time in which all three could get to the end of their journey?”
See the Tandem Bicycle Puzzle for a solution.
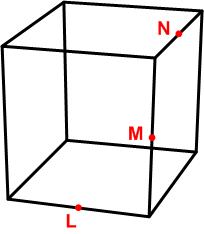 This is from the UKMT Senior Challenge of 2004.
This is from the UKMT Senior Challenge of 2004.
“L, M, and N are midpoints of a skeleton cube, as shown. What is the value of angle LMN?
_____A_90°_____B_105°_____C_120°_____D_135°_____E_150°”
See Cube Slice Angle Problem for solutions.
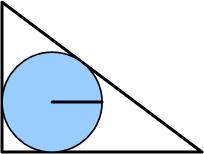 This statement showed up recently at Futility Closet and I found it to be another one of those magical results that seemed so surprising. I don’t recall ever seeing this before.
This statement showed up recently at Futility Closet and I found it to be another one of those magical results that seemed so surprising. I don’t recall ever seeing this before.
“The radius of a circle inscribed in a 3-4-5 triangle is 1.
(In fact, the inradius of any Pythagorean triangle is an integer.)”
(A Pythagorean triangle is a right triangle whose sides form a Pythagorean triple.) Futility Closet left these remarkable statements unproven, so naturally I felt I had to provide a proof.
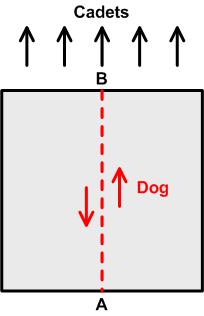 In my search for new problems I came across this one from Martin Gardner:
In my search for new problems I came across this one from Martin Gardner:
“A square formation of Army cadets, 50 feet on the side, is marching forward at a constant pace [see Figure]. The company mascot, a small terrier, starts at the center of the rear rank [position A in the illustration], trots forward in a straight line to the center of the front rank [position B], then trots back again in a straight line to the center of the rear. At the instant he returns to position A, the cadets have advanced exactly 50 feet. Assuming that the dog trots at a constant speed and loses no time in turning, how many feet does he travel?”
Gardner gives a follow-up problem that is virtually impossible:
“If you solve this problem, which calls for no more than a knowledge of elementary algebra, you may wish to tackle a much more difficult version proposed by the famous puzzlist Sam Loyd. Instead of moving forward and back through the marching cadets, the mascot trots with constant speed around the outside of the square, keeping as close as possible to the square at all times. (For the problem we assume that he trots along the perimeter of the square.) As before, the formation has marched 50 feet by the time the dog returns to point A. How long is the dog’s path?”
See the Marching Cadets and Dog Problem for solutions.
 This is a delightful little problem from Dick Hess that exercises one’s basic facility with logarithms:
This is a delightful little problem from Dick Hess that exercises one’s basic facility with logarithms:
“Define x as ![]()
Find an expression for ![]()
in terms of x where the only constants appearing are integers.”
See the Logging Problem for a solution.
 I was reading yet another book on the Scientific Revolution when I came across a discussion of the mathematical significance of the invention of perspective for painting in the 15th century Italian Renaissance. The main player in the saga was Leon Battista Alberti (1404 – 1472) and his tome De Pictura (On Painting) (1435-6), which contained the first mathematical presentation of perspective. Even though mathematics was advertised, it was not at the level of trigonometry I used in my post “The Perspective Map”, but rather entailed simple Euclidean plane geometry. So the discussion was largely historical rather than mathematical. Nevertheless, I became curious to learn how much Alberti was able to discover about perspective without a lot of math. This essay is the result.
I was reading yet another book on the Scientific Revolution when I came across a discussion of the mathematical significance of the invention of perspective for painting in the 15th century Italian Renaissance. The main player in the saga was Leon Battista Alberti (1404 – 1472) and his tome De Pictura (On Painting) (1435-6), which contained the first mathematical presentation of perspective. Even though mathematics was advertised, it was not at the level of trigonometry I used in my post “The Perspective Map”, but rather entailed simple Euclidean plane geometry. So the discussion was largely historical rather than mathematical. Nevertheless, I became curious to learn how much Alberti was able to discover about perspective without a lot of math. This essay is the result.
See Alberti’s Perspective Construction
(Update 7/29/2019) I got a response! Continue reading
This is problem #25 from the UKMT 2014 Senior Challenge.
“Figure 1 shows a tile in the form of a trapezium [trapezoid], where a = 83⅓°. Several copies of the tile placed together form a symmetrical pattern, part of which is shown in Figure 2. The outer border of the complete pattern is a regular ‘star polygon’. Figure 3 shows an example of a regular ‘star polygon’.
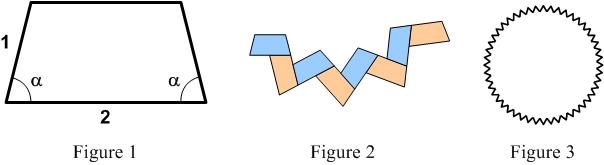 How many tiles are there in the complete pattern?
How many tiles are there in the complete pattern?
_____A_48_____B_54_____C_60_____D_66_____E_72”
See the Star Polygon Problem for solutions.
 This is another delightful H. E. Dudeney puzzle.
This is another delightful H. E. Dudeney puzzle.
“Mr. Gubbins, a diligent man of business, was much inconvenienced by a London fog. The electric light happened to be out of order and he had to manage as best he could with two candles. His clerk assured him that though both were of the same length one candle would burn for four hours and the other for five hours. After he had been working some time he put the candles out as the fog had lifted, and he then noticed that what remained of one candle was exactly four times the length of what was left of the other.
When he got home that night Mr. Gubbins, who liked a good puzzle, said to himself, ‘Of course it is possible to work out just how long those two candles were burning to-day. I’ll have a shot at it.’ But he soon found himself in a worse fog than the atmospheric one. Could you have assisted him in his dilemma? How long were the candles burning?”
See Mr. Gubbins in a Fog for a solution.
 In a June Chalkdust book review of Daniel Griller’s second book, Problem solving in GCSE mathematics, Matthew Scroggs presented the following problem #65 from the book (without a solution):
In a June Chalkdust book review of Daniel Griller’s second book, Problem solving in GCSE mathematics, Matthew Scroggs presented the following problem #65 from the book (without a solution):
“Solve _______________![]() ”
”
Scroggs’s initial reaction to the problem was “it took me a while to realise that I even knew how to solve it.”
Mind you, according to Wikipedia, “GCSEs [General Certificate of Secondary Education] were introduced in 1988 [in the UK] to establish a national qualification for those who decided to leave school at 16, without pursuing further academic study towards qualifications such as A-Levels or university degrees.” My personal feeling is that any student who could solve this problem should be encouraged to continue their education with a possible major in a STEM field.
See Cube Roots Problem for a solution.