 The Columbus story shows the intervention of chance in history at its most capricious. The following tale has its own logic, but the confluence of serendipitous events makes it marvelous and uplifting, especially in our current dark times. It was first brought to my attention by my father back in the early 1960s at the height of America’s role as wheat breadbasket of the world. America, and especially Kansas, was supplying essential wheat to the recently independent country of India and to the Soviet Union, whose long struggle with collective farming (and other factors), especially in the Ukraine, had led to its dependency on imports.
The Columbus story shows the intervention of chance in history at its most capricious. The following tale has its own logic, but the confluence of serendipitous events makes it marvelous and uplifting, especially in our current dark times. It was first brought to my attention by my father back in the early 1960s at the height of America’s role as wheat breadbasket of the world. America, and especially Kansas, was supplying essential wheat to the recently independent country of India and to the Soviet Union, whose long struggle with collective farming (and other factors), especially in the Ukraine, had led to its dependency on imports.
I will not try to narrate the story O’Henry-like with a surprise ending, but announce the amazing coincidence from the start—America was supplying the USSR its own wheat! The Kansas wheat was derived from a special hardy winter variety called Turkey Red that had originated in the Ukraine and was brought to America by Mennonites. So the story is how this all came about. See Turkey Red.
(Update 2/24/2022) Russian Invasion of Ukraine
More ironic coincidences. Who would have thought a story about wheat from a distant land over one hundred years ago would become timely in the 21st century. But terms like Catherine the Great’s “New Russia” are being uttered by a modern despot Vladimir Putin and port cities like Mariupol are again in the news. All attention has been on focused on the effect of Putin’s folly on oil and gas, but I have been wondering about its consequences for the wheat. And sure enough, such concerns are finally in the news.
See the Russian Invasion.
(Update 2/28/2022) Russia May Weaponize Food Supply Chain
Politico has a more expansive article on the implications of the grain production in Ukraine by Ian Ralby et al., “Why the U.S. Needs to Act Fast to Prevent Russia from Weaponizing Food Supply Chains”. For example, the article asserts, “Amid the chaos of this conflict and the threat to Ukrainian lives and independence, one critical implication has been grossly underexamined: how Russia could rely on China’s support to weaponize global food supply chains.” Though Russia’s gas and oil production has garnered the most attention, “Russia’s control of Ukrainian grain shipments will likely have far greater consequences. After just one day of the invasion, Russia effectively controlled nearly a third of the world’s wheat exports, three quarters of the world’s sunflower oil exports, and substantial amounts of barley, soy and other grain supply chains.” The article examines in detail the implications of this control.
See Russia and Food Supply Chain.
 Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:
Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:
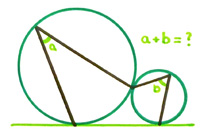 I really was trying to stop including
I really was trying to stop including  An amazing publication was conceived primarily for women at the beginning of the 18th century in 1704 and was called The Ladies’ Diary or Woman’s Almanack. What made it even more remarkable was that each issue contained mathematical problems whose solutions from the readers were provided in the next issue. One particularly sharp woman was Mary Wright (Mrs. Mary Nelson). This is one of her problems:
An amazing publication was conceived primarily for women at the beginning of the 18th century in 1704 and was called The Ladies’ Diary or Woman’s Almanack. What made it even more remarkable was that each issue contained mathematical problems whose solutions from the readers were provided in the next issue. One particularly sharp woman was Mary Wright (Mrs. Mary Nelson). This is one of her problems: This is another train puzzle from H. E. Dudeney, which is fairly straight-forward.
This is another train puzzle from H. E. Dudeney, which is fairly straight-forward. The
The 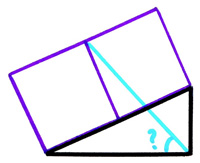 Since everyone by now who has any interest has gone directly to Catriona Shearer’s Twitter account for geometric puzzles, I was not going to include any more. But this one with its one-step solution is too fine to ignore and belongs with the “5 Problem” as one of the most elegant.
Since everyone by now who has any interest has gone directly to Catriona Shearer’s Twitter account for geometric puzzles, I was not going to include any more. But this one with its one-step solution is too fine to ignore and belongs with the “5 Problem” as one of the most elegant.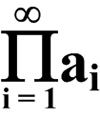 This is a challenging problem from Mathematical Quickies (1967).
This is a challenging problem from Mathematical Quickies (1967).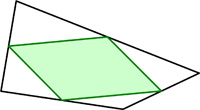 I came across this problem in Alfred Posamentier’s book, but I remember I had seen it a couple of places before and had never thought to solve it. At first, it seems like magic.
I came across this problem in Alfred Posamentier’s book, but I remember I had seen it a couple of places before and had never thought to solve it. At first, it seems like magic.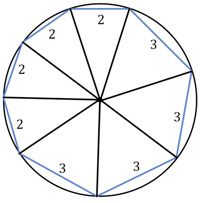 Here is a problem from the famous (infamous?) Putnam exam, presented by Presh Talwalkar. Needless to say, I did not solve it in 30 minutes—but at least I solved it (after making a blizzard of arithmetic and trigonometric errors).
Here is a problem from the famous (infamous?) Putnam exam, presented by Presh Talwalkar. Needless to say, I did not solve it in 30 minutes—but at least I solved it (after making a blizzard of arithmetic and trigonometric errors).