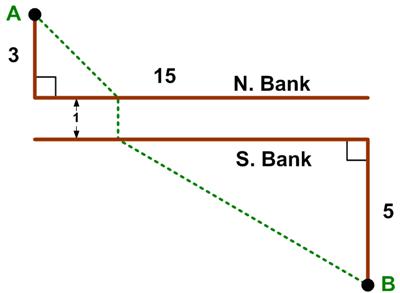
 This is a riff on a classic problem, given in Challenging Problems in Algebra.
This is a riff on a classic problem, given in Challenging Problems in Algebra.
“N. Bank and S. Bank are, respectively, the north and south banks of a river with a uniform width of one mile. Town A is 3 miles north of N. Bank, town B is 5 miles south of S. Bank and 15 miles east of A. If crossing at the river banks is only at right angles to the banks, find the length of the shortest path from A to B.
Challenge. If the rate of land travel is uniformly 8 mph, and the rowing rate on the river is 1 2/3 mph (in still water) with a west to east current of 1 1/3 mph, find the shortest time it takes to go from A to B. [The path across the river must still be perpendicular to the banks.]”
Answer.
See the River Crossing for a solution.
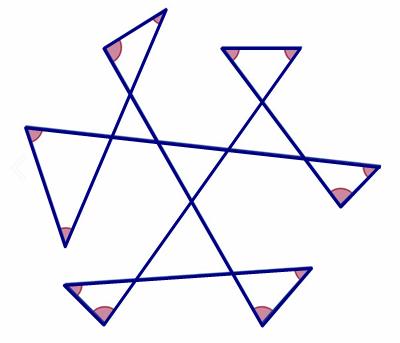 Mathnasium of Amarillo had a nice follow up on the sum of angles type of puzzle.
Mathnasium of Amarillo had a nice follow up on the sum of angles type of puzzle.
 This is a riff on a classic problem, given in Challenging Problems in Algebra.
This is a riff on a classic problem, given in Challenging Problems in Algebra.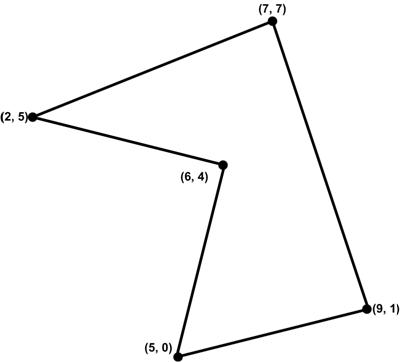 This is another problem from
This is another problem from 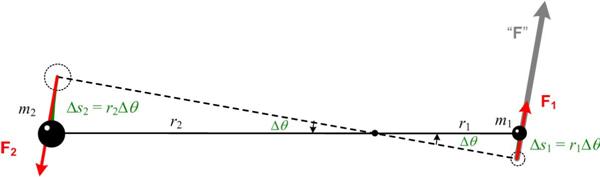 I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his
I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his 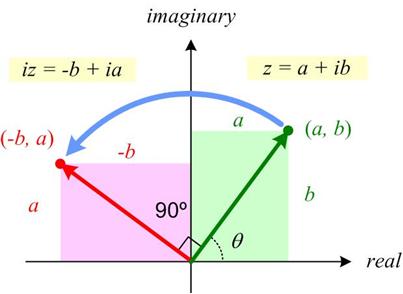 This may be a futile attempt at an elementary introduction to complex variables by emphasizing their geometric properties. The elementary part is probably undermined by an initial discussion of field extensions and a necessary reference to trigonometry. Hopefully, the suppression of the explicit use of complex powers of Euler’s constant e until the very end will allow the geometric ideas to have center stage. A primary goal of the essay is to realize that complex polynomials involve sums of circles in the plane. The image of real polynomials as wavy curves in the plane is misleading for an understanding of complex behavior. See
This may be a futile attempt at an elementary introduction to complex variables by emphasizing their geometric properties. The elementary part is probably undermined by an initial discussion of field extensions and a necessary reference to trigonometry. Hopefully, the suppression of the explicit use of complex powers of Euler’s constant e until the very end will allow the geometric ideas to have center stage. A primary goal of the essay is to realize that complex polynomials involve sums of circles in the plane. The image of real polynomials as wavy curves in the plane is misleading for an understanding of complex behavior. See 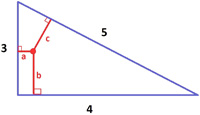 James Tanton
James Tanton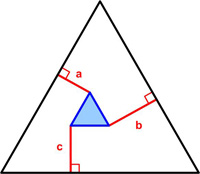 I found this collection of related problems by
I found this collection of related problems by 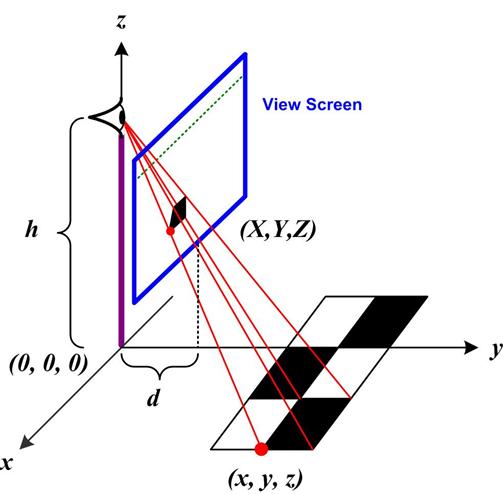 A number of recent puzzles have involved perspective views of objects. I had never really explored the idea of a perspective map in detail. So some of the properties associated with it always seemed a bit vague to me. I decided I would derive the mathematical equations for the perspective or projective map and see how its properties fell out from the equations. With this information in hand I then addressed some questions I had about the article “Dürer: Disguise, Distance, Disagreements, and Diagonals!” by Annalisa Crannell, Marc Frantz, and Fumiko Futamura concerning a controversy over Albrecht Dürer’s woodcut St. Jerome in His Study (1514). And finally, I read somewhere that a parabola under a perspective map becomes an ellipse, so I was able to show that as well. See the
A number of recent puzzles have involved perspective views of objects. I had never really explored the idea of a perspective map in detail. So some of the properties associated with it always seemed a bit vague to me. I decided I would derive the mathematical equations for the perspective or projective map and see how its properties fell out from the equations. With this information in hand I then addressed some questions I had about the article “Dürer: Disguise, Distance, Disagreements, and Diagonals!” by Annalisa Crannell, Marc Frantz, and Fumiko Futamura concerning a controversy over Albrecht Dürer’s woodcut St. Jerome in His Study (1514). And finally, I read somewhere that a parabola under a perspective map becomes an ellipse, so I was able to show that as well. See the  This is another
This is another  Years ago (1963) I got the paperback The Calculus:A Genetic Approach, by Otto Toeplitz, which presented the basic ideas of the differential and integral calculus from a historical point of view. One thing Toeplitz did at the end of his book that I had not seen in other texts was to show the equivalence of Kepler’s Laws and Newton’s Law of Gravity. (Since 1963 David Bressoud has developed this theme in his excellent 1991 text.) I thought I would try to emulate Toeplitz’s approach with more modern notation (vectors) and arguments in hopes of extracting the essential ideas from the clutter.
Years ago (1963) I got the paperback The Calculus:A Genetic Approach, by Otto Toeplitz, which presented the basic ideas of the differential and integral calculus from a historical point of view. One thing Toeplitz did at the end of his book that I had not seen in other texts was to show the equivalence of Kepler’s Laws and Newton’s Law of Gravity. (Since 1963 David Bressoud has developed this theme in his excellent 1991 text.) I thought I would try to emulate Toeplitz’s approach with more modern notation (vectors) and arguments in hopes of extracting the essential ideas from the clutter.