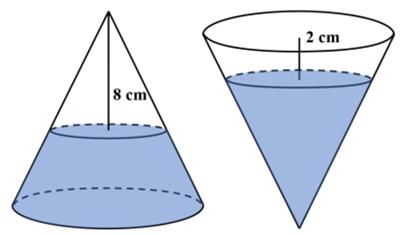
 I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.
I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.
Presh Talwalkar: “This was sent to me as a competition problem for 8th graders, so it would be a challenge problem for students aged 12 to 13. When a conical bottle rests on its flat base, the water in the bottle is 8 cm from its vertex. When the same conical bottle is turned upside down, the water level is 2 cm from its base. What is the height of the bottle? (Note “conical” refers to a right circular cone as is common usage.) I at first thought this problem was impossible. But it actually can be solved.”
See the Conical Bottle Problem for solutions.

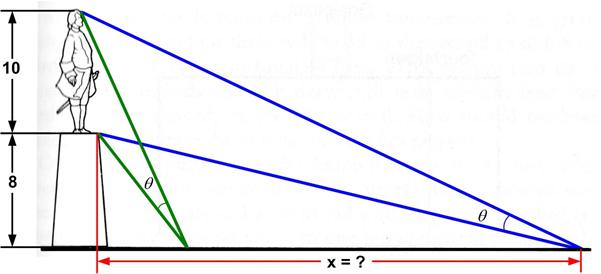 This is an old problem I had seen before. Here is David Wells’s rendition:
This is an old problem I had seen before. Here is David Wells’s rendition: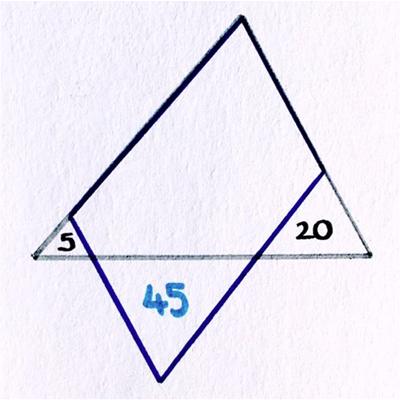
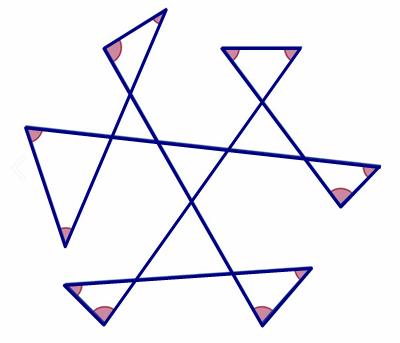
 This is a riff on a classic problem, given in Challenging Problems in Algebra.
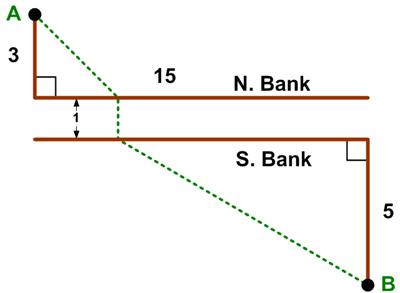
This is a riff on a classic problem, given in Challenging Problems in Algebra.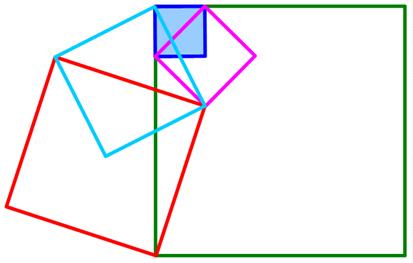 Here is another imaginative geometry problem from
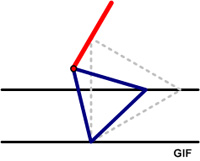
Here is another imaginative geometry problem from 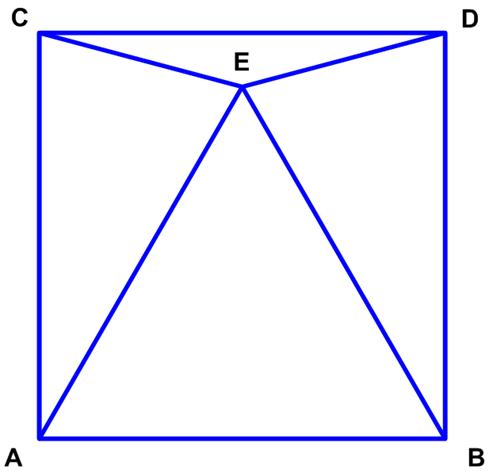 The issue 7 of the Chalkdust mathematics magazine had an interesting geometric problem presented by Matthew Scroggs.
The issue 7 of the Chalkdust mathematics magazine had an interesting geometric problem presented by Matthew Scroggs.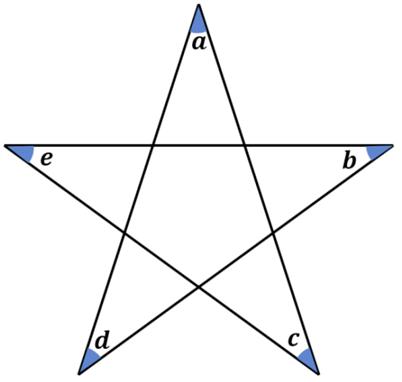 This problem posted by Presh Talwalkar offers a variety of solutions, but I didn’t quite see my favorite approach for such problems. So I thought I would add it to the mix.
This problem posted by Presh Talwalkar offers a variety of solutions, but I didn’t quite see my favorite approach for such problems. So I thought I would add it to the mix.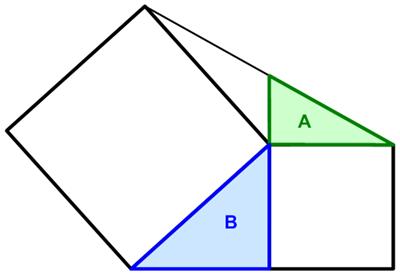 This was a nice geometric problem from Poo-Sung Park
This was a nice geometric problem from Poo-Sung Park