 This is another challenging sum from the 2024 Math Calendar.
This is another challenging sum from the 2024 Math Calendar.
“Find x where x = et and
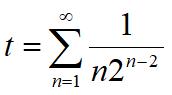 ”
”
As before, recall that all the answers are integer days of the month.
See Yet Another Sum for a solution.

 This is another challenging sum from the 2024 Math Calendar.
This is another challenging sum from the 2024 Math Calendar.
“Find x where x = et and
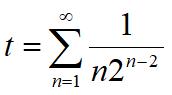 ”
”
As before, recall that all the answers are integer days of the month.
See Yet Another Sum for a solution.
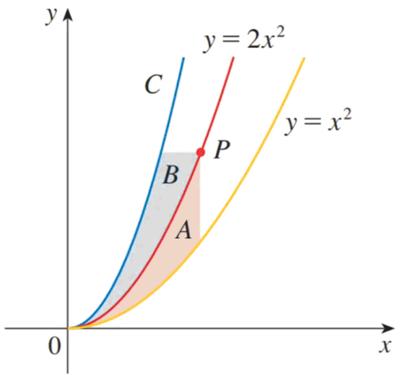 Here is another problem from BL’s Weekly Math Games.
Here is another problem from BL’s Weekly Math Games.
“For every point P on y = 2x2, areas A and B are equal. Find the equation for curve C.”
See Mystery Curve Puzzle for a solution
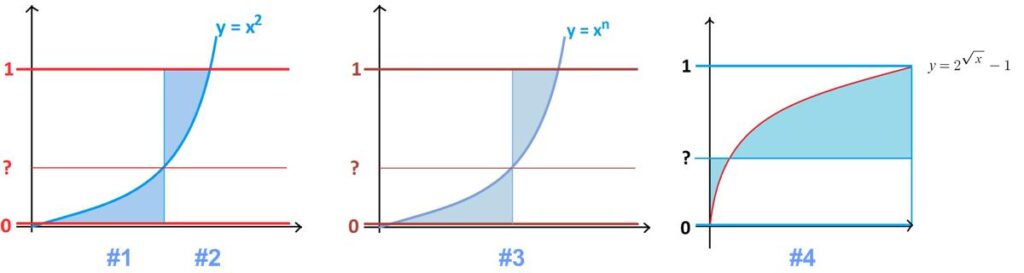 A while ago James Tanton provided a series of puzzles:
A while ago James Tanton provided a series of puzzles:
Puzzle #1 At what value between 0 and 1 does a horizontal line at that height produce two regions of equal area as shown on the graph of y = x2?
Puzzle #2 A horizontal line is drawn between the lines y = 0 and y = 1, dividing the graph of y = x2 into two regions as shown. At what height should that line be drawn so that the sum of the areas of these two regions is minimal?
Puzzle #3 A horizontal line is drawn between the lines y = 0 and y = 1, dividing the graph of y = xn into two regions as shown (n > 0). At what height should that line be drawn so that the sum of the areas of these two regions is minimal? Does that height depend on the value of n?
Puzzle #4 What horizontal line drawn between y = 0 and y = 1 on the graph of y = 2√x – 1 minimizes the sum of the two shaded areas shown?
See Double Areas Puzzles for solutions.
 Here is a fairly computationally challenging 1994 AIME problem .
Here is a fairly computationally challenging 1994 AIME problem .
“Find the positive integer n for which
⌊log2 1⌋ + ⌊log2 2⌋ + ⌊log2 3⌋ + … + ⌊log2 n⌋ = 1994.
where for real x, ⌊x⌋ is the greatest integer ≤ x.”
There is some fussy consideration of indices.
See the Special Log Sum for a solution.
 Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
_______________
As before, recall that all the answers are integer days of the month.
See the Amazing Root Problem for a solution.
 This is yet another series offered by Presh Talwalkar.
This is yet another series offered by Presh Talwalkar.
“What is the value of the following sum?
____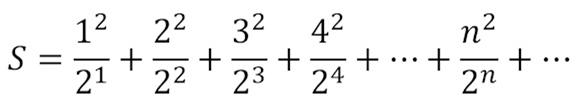
Talwalkar gives hints for three possible approaches to the solution.
See Another Challenging Sum for solutions.
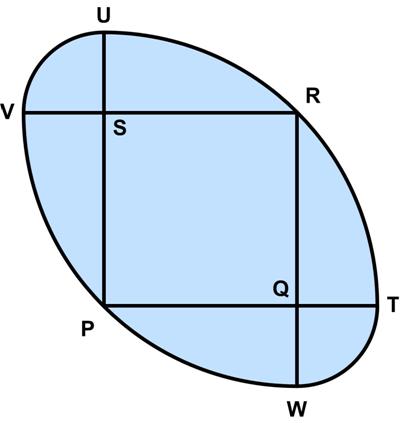 Here is another UKMT Senior Challenge problem for 2017.
Here is another UKMT Senior Challenge problem for 2017.
“The diagram shows a square PQRS with edges of length 1, and four arcs, each of which is a quarter of a circle. Arc TRU has centre P; arc VPW has centre R; arc UV has centre S; and arc WT has centre Q.
What is the length of the perimeter of the shaded region?
A_6___B_(2√2 – 1)π___C_(√2 – 1/2)π ___D_2___E_(3√2 – 2)π”
See Elliptic Circles for a solution.
 This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
“31. Prove that if n is a natural number, then we have
(√2 – 1)n = √m – √(m – 1),
where m is a natural number.”
Here, natural numbers are 1, 2, 3, …
I found it to be quite challenging, as all the Polish Math Olympiad problems seem to be.
See the Amazing Identity
 Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem.
Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem.
“A cyclist sets off from point O and rides with constant velocity v along a rectilinear highway. A messenger, who is at a distance a from point O and at a distance b from the highway, wants to deliver a letter to the cyclist. What is the minimum velocity with which the messenger should run in order to attain his objective?”
See the Tired Messenger Problem
(Update 1/29/2025) Dan Steinitz Solution
Dan Steinitz from Israel has sent an elegant solution that only involves vectors and geometry without calculus. I have edited slightly his email and added excerpts from his whiteboard solution, though without the Hebrew annotations, which unfortunately I cannot read. But that is the glory of the universal language of mathematics: it can be read and understood in any language.
 Here is another typical sum puzzle from Presh Talwalkar.
Here is another typical sum puzzle from Presh Talwalkar.
“Solve the following sums:
_____1/(1×3) + 1/(3×5) + 1/(5×7) + 1/(7×9) + 1/(9×11) =
_____1/(4×7) + 1/(7×10) + 1/(10×13) + 1/(13×16) =
_____1/(2×7) + 1/(7×12) + 1/(12×17) + … =”
The only reason I am including this puzzle is that Talwalkar gets very excited about deriving a formula that can solve sums of this type. This gives me an opportunity to discuss the “formula vs. procedure” way of doing math.
See the Incredible Trick Puzzle for solutions.