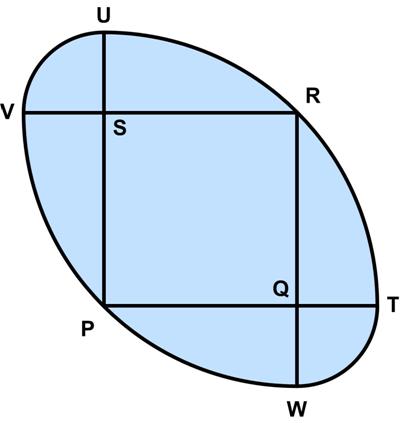
Here is another UKMT Senior Challenge problem for 2017.
“The diagram shows a square PQRS with edges of length 1, and four arcs, each of which is a quarter of a circle. Arc TRU has centre P; arc VPW has centre R; arc UV has centre S; and arc WT has centre Q.
What is the length of the perimeter of the shaded region?
A_6___B_(2√2 – 1)π___C_(√2 – 1/2)π ___D_2___E_(3√2 – 2)π”
See Elliptic Circles for a solution.
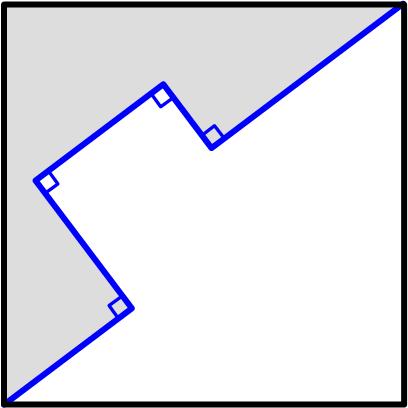This is a nice problem from the UKMT Senior Mathematics Challenge for 2022:
“Five line segments of length 2, 2, 2, 1 and 3 connect two corners of a square as shown in the diagram. What is the shaded area?
A 8____B 9____C 10____D 11____E 12”
The pleasure of solving this problem may be lessened if one is under a time crunch, as is the case with all these timed tests.
See the Broken Diagonal Problem for solutions.
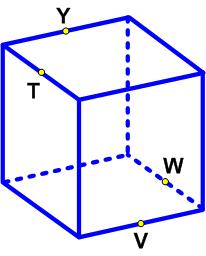This is a problem from the UKMT Senior Challenge for 2019. (It has been slightly edited to reflect the colors I added to the diagram.)
“The edge-length of the solid cube shown is 2. A single plane cut goes through the points Y, T, V and W which are midpoints of the edges of the cube, as shown.
What is the area of the cross-section?
A_√3_____B_3√3_____C_6_____D_6√3_____E_8”
See Another Cube Slice Problem for solutions.
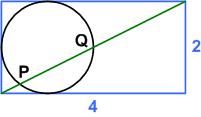Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution:
“The diagram shows a circle of radius 1 touching three sides of a 2 x 4 rectangle. A diagonal of the rectangle intersects the circle at P and Q, as shown.
What is the length of the chord PQ?
__A_√5____B_4/√5____C_√5 – 2/√5____D_5√5/6____E_2”
See the Circle in Slot Problem for a solution.
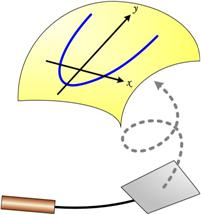This is a stimulating problem from the UKMT Senior Math Challenge for 2017. The additional problem “for investigation” is particularly challenging. (I have edited the problem slightly for clarity.)
“The parabola with equation y = x² is reflected about the line with equation y = x + 2. Which of the following is the equation of the reflected parabola?
A_x = y² + 4y + 2_____B_x = y² + 4y – 2_____C_x = y² – 4y + 2
D_x = y² – 4y – 2_____E_x = y² + 2
For investigation: Find the coordinates of the point that is obtained when the point with coordinates (x, y) is reflected about the line with equation y = mx + b.”
See Flipping Parabolas for a solution.
This is from the UKMT Senior Challenge of 2004.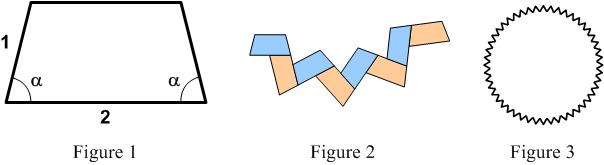
“L, M, and N are midpoints of a skeleton cube, as shown. What is the value of angle LMN?
_____A_90°_____B_105°_____C_120°_____D_135°_____E_150°”
See Cube Slice Angle Problem for solutions.
This is problem #25 from the UKMT 2014 Senior Challenge.
“Figure 1 shows a tile in the form of a trapezium [trapezoid], where a = 83⅓°. Several copies of the tile placed together form a symmetrical pattern, part of which is shown in Figure 2. The outer border of the complete pattern is a regular ‘star polygon’. Figure 3 shows an example of a regular ‘star polygon’.
How many tiles are there in the complete pattern?
_____A_48_____B_54_____C_60_____D_66_____E_72”
See the Star Polygon Problem for solutions.
This is from the UKMT Senior Challenge of 1999.
What is the sum to infinity of the convergent series
A_7/4_____B_2_____C_√5_____D_9/4_____E_7/3”
See Fibonacci Fandango for a solution.
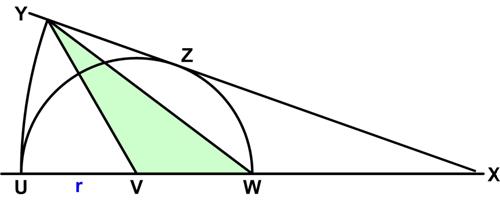Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:
“A semicircle of radius r is drawn with centre V and diameter UW. The line UW is then extended to the point X, such that UW and WX are of equal length. An arc of the circle with centre X and radius 4r is then drawn so that the line XY is tangent to the semicircle at Z, as shown. What, in terms of r, is the area of triangle YVW?”
See the Rising Sun for solutions.
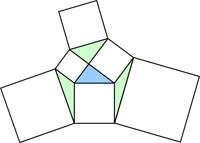This is a problem from the UKMT Senior Challenge for 2001. (It has been slightly edited to reflect the colors I added to the diagram.)
“The [arbitrary] blue triangle is drawn, and a square is drawn on each of its edges. The three green triangles are then formed by drawing their lines which join vertices of the squares and a square is now drawn on each of these three lines. The total area of the original three squares is A1, and the total area of the three new squares is A2. Given that A2 = k A1, then
_____A_ k = 1_____B_ k = 3/2_____C_ k = 2_____D_ k = 3_____E_ more information is needed.”
I solved this problem using a Polya principle to simplify the situation, but UKMT’s solution was direct (and more complicated).
See the Six Squares Problem for solutions.
