Tag Archives: UKMT Challenge

Hitting the Target

Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:

“Tom and Geri have a competition. Initially, each player has one attempt at hitting a target. If one player hits the target and the other does not then the successful player wins. If both players hit the target, or if both players miss the target, then each has another attempt, with the same rules applying. If the probability of Tom hitting the target is always 4/5 and the probability of Geri hitting the target is always 2/3, what is the probability that Tom wins the competition?

______A 4/15______B 8/15______C 2/3______D 4/5______E 13/15”

Answer.

See Hitting the Target for solutions.

Challenging Sum

Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2009:

“Four positive integers a, b, c, and d are such that

abcd + abc + bcd + cda + dab + ab + bc + cd + da + ac + bd + a + b + c + d = 2009.

What is the value of a + b + c + d?

A 73_________B 75_________C 77_________D 79_________E 81”

Answer.

See the Challenging Sum for a solution.

(Update 4/17/2019) Continue reading →

More Pool

This is another UKMT Senior Challenge problem, this time from 2006.

“A toy pool table is 6 feet long and 3 feet wide. It has pockets at each of the four corners P, Q, R, and S. When a ball hits a side of the table, it bounces off the side at the same angle as it hit that side. A ball, initially 1 foot to the left of pocket P, is hit from the side SP towards the side PQ as shown. How many feet from P does the ball hit side PQ if it lands in pocket S after two bounces?”

Pool Partiers should have no difficulty solving this.

Answer.

See More Pool for solutions.

Right Triangle with Roots

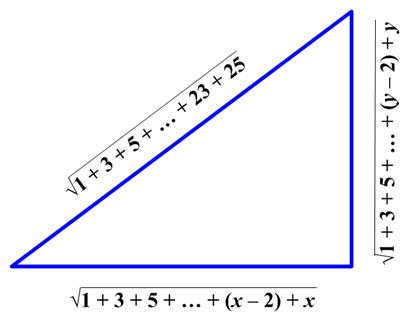This is an interesting problem from the United Kingdom Mathematics Trust (UKMT) Senior Math Challenge of 2008.

“The length of the hypotenuse of a particular right-angled triangle is given by √(1 + 3 + 5 + … + 23 + 25). The lengths of the other two sides are given by √(1 + 3 + 5 + … + (x – 2) + x) and √ (1 + 3 + 5 + … + (y – 2) + y) where x and y are positive integers. What is the value of x + y?”

Answer.

See the Right Triangle with Roots for a solution.

  1. Pages:
  3. 1
  4. 2